Modelos Lineales
The slides are available here!
Esta clase profundiza en los modelos de clasificación lineal, mostrando cómo un hiperplano puede separar ejemplos en un espacio de características. Además, se introduce la regresión lineal como un caso particular de modelos lineales (cuando la variable a predecir es continua) y la regresión logística (para valores binarios o multi-clase). Finalmente, veremos una introducción al uso de scikit-learn, la librería de Python muy popular para Machine Learning.
(Para el orador: Puedes enfatizar en las propiedades de la linealidad, la noción de hiperplano, la forma de pasar a modelos más complejos con un truco de aumento del espacio, y rematar con ejemplos en scikit-learn. Invita a la discusión de por qué a veces preferimos estos modelos lineales frente a otros más complejos.)
Modelos de Clasificación
Clasificador lineal
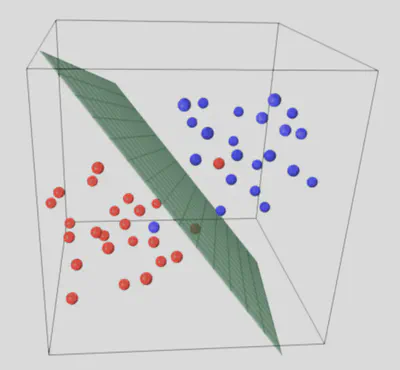
El objetivo de un clasificador lineal es separar el espacio de atributos con un hiperplano de manera que queden los ejemplos de una clase a un lado y los de la(s) otra(s) clase(s) al otro lado.
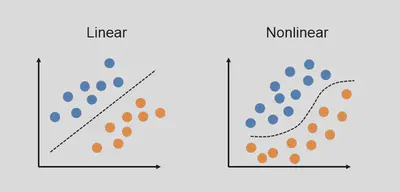
Problemas lineales vs. no lineales
En la práctica, muchas fronteras de decisión no son lineales. Sin embargo, aún podemos aplicar modelos lineales si creamos características más elaboradas o hacemos transformaciones adecuadas.
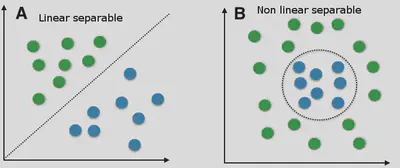
- Una función $f : \mathcal{X}\rightarrow \mathcal{Y}$ es lineal si $f(\lambda \mathbf{x} + \mathbf{x}') = \lambda\,f(\mathbf{x}) + f(\mathbf{x}')$ .
- Un caso típico es $f(\mathbf{x}) = \theta^T \mathbf{x} = \sum_i \theta_i\,x_i$ .
Hiperplano (geometría)
Para $\mathbf{x} \in \mathbb{R}^d$ , un hiperplano $\mathcal{H}$ está definido por ecuaciones tipo:
$$ w_1\,x_1 \;+\; w_2\,x_2 \;+\;\dots\;+\; w_d\,x_d \;+\; w_0 \;=\; 0. $$Interpretación: el signo de $w_1 x_1 + \dots + w_d x_d + w_0$ indica de qué lado del hiperplano se encuentra $\mathbf{x}$ .
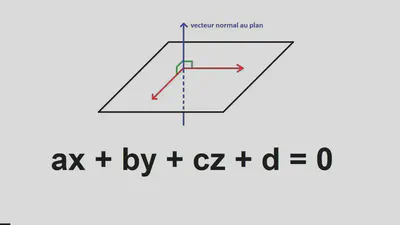
(Para el orador: Recordar que, en 2D, se llama recta; en 3D, se llama plano; y en más dimensiones, se sigue llamando hiperplano.)
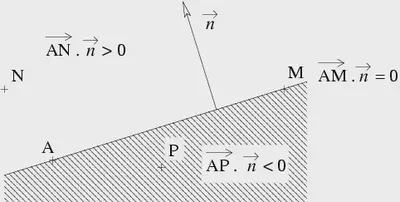
En este diagrama vemos cómo la normal ($\vec{n}$ ) al hiperplano define su orientación. El término $w_0$ (o sesgo) desplaza el plano.
Producto escalar y parte afín
Si aumentamos el espacio añadiendo un 1 a nuestro vector de características: $ \mathbf{x} \;=\; \begin{pmatrix} x_1\\ \vdots\\ x_d\\ 1 \end{pmatrix},\quad \theta \;=\; \begin{pmatrix} \theta_1\\ \vdots\\ \theta_d\\ \theta_0 \end{pmatrix}, $ entonces $\theta^T \mathbf{x} = w_0 + \sum_i w_i\,x_i$ . Esto permite manejar en un mismo marco la parte “afín” del hiperplano.
Resumen
El clasificador lineal más sencillo se define como:
$$ f_{\mathbf{W}, b}(\mathbf{x}) \;=\; \begin{cases} +1, & \text{si } (\mathbf{W}^T\,\mathbf{x} + b)\;\ge\;0, \\ -1, & \text{en caso contrario}. \end{cases} $$O, en problemas multiclase, usamos la misma idea (hiperplano para cada clase) y elegimos la que tenga la salida más alta (argmax).
(Para el orador: Recalca cómo, si no es separable linealmente, podemos usar un truco de “features” que nos lleven a un espacio donde sí lo sea.)
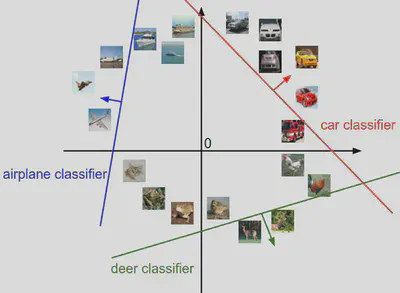
Clasificador lineal multinomial
Para más de 2 clases, podemos tener una matriz $\mathbf{W}$ , donde cada fila corresponde a un posible “hiperplano” que da una puntuación a la clase. Luego:
$$ \hat{c}(\mathbf{x}) \;=\; \arg\max_{c}\;\bigl(\mathbf{W}_c^T\,\mathbf{x} + b_c\bigr). $$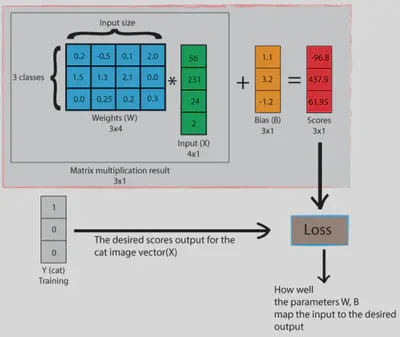
(Para el orador: destacar que es una operación muy rápida, pues es un producto matriz-vector.)
Integración del sesgo
En vez de $\mathbf{W}^T\mathbf{x} + b$ , se pasa a un producto escalar extendido:
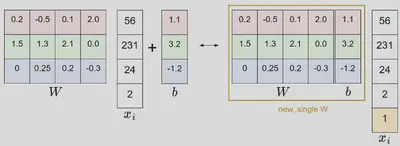
Aumento del espacio para no linealidad
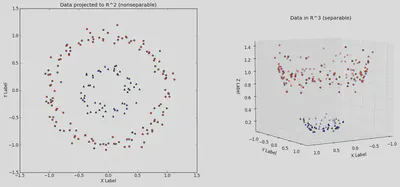
Se puede agregar variables no lineales (por ejemplo $z = x^2 + y^2$ ) para separar datos no linealmente separables en la dimensión original. La separación sigue siendo lineal en el espacio de mayor dimensión.
Regresión Lineal
La Regresión Lineal es un modelo lineal para predecir una variable continua $y$ . En su forma más simple en 1D:
$$ \hat{y} \;=\; w\,x \;+\; b. $$O en multidimensional:
$$ \hat{y} \;=\; \mathbf{W}^T\,\mathbf{x} \;+\; b. $$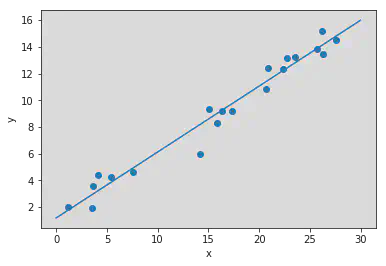
Métricas en regresión
Para estimar la calidad de la predicción:
- Error Medio Absoluto: $\frac{1}{n}\sum \bigl|Y_i - f(\mathbf{X}_i)\bigr|$
- Error Cuadrático Medio: $\frac{1}{n}\sum \bigl(Y_i - f(\mathbf{X}_i)\bigr)^2$
- Coeficiente de determinación $R^2$ , que mide cuánta varianza de $Y$ explica el modelo.
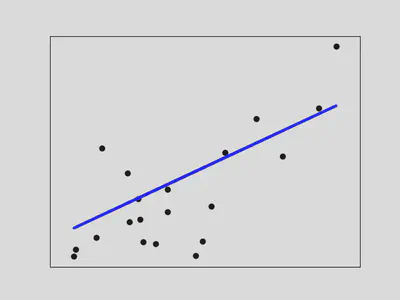
(Para el orador: Explica la interpretación de $R^2$ como fracción de varianza explicada.)
Regresión de un plano en 3D
Para dos atributos $x_1, x_2$ y una salida $y$ :
$$ \hat{y} \;=\; w_1\,x_1 \;+\; w_2\,x_2 \;+\; b. $$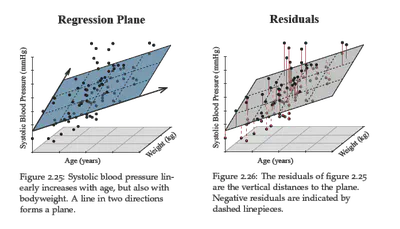
Regresión Logística
La regresión logística (en su forma binaria) se utiliza para convertir una salida lineal (o “distancia” en el espacio de características) en una probabilidad entre 0 y 1. Además, en el caso multiclase, se generaliza a la llamada función softmax, la cual asigna una probabilidad a cada clase, de modo que la suma de todas las probabilidades es igual a 1.
Caso Binario
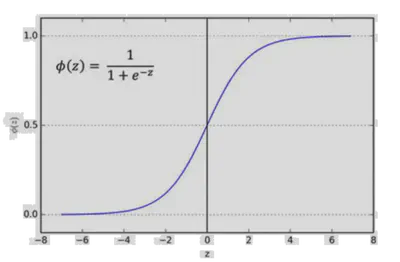
ara problemas de clasificación binaria, la regresión logística aplica la función sigmoide o softmax sobre la salida lineal. La idea principal es definir una función sigmoide que proyecte cualquier valor real (la salida lineal $\mathbf{W}^T \mathbf{x} + b$ ) a un rango de $]0, 1[$ :
$$ \sigma(z) \;=\; \frac{1}{1 + e^{-z}} $$- Cuando $z \rightarrow +\infty$ , la sigmoide se acerca a 1.
- Cuando $z \rightarrow -\infty$ , la sigmoide se acerca a 0.
En regresión logística binaria (dos clases), llamemos “1” a la clase positiva y “0” (o “-1”) a la negativa. Entonces la probabilidad de que un ejemplo $\mathbf{x}$ sea de la clase positiva es:
$$ P(Y = 1 \;|\; \mathbf{x}) \;=\; \sigma\bigl(\mathbf{W}^T\mathbf{x} + b\bigr) \;=\; \frac{1}{1 + e^{-(\mathbf{W}^T\mathbf{x} + b)}}. $$Por ende, $P(Y=0 \;|\; \mathbf{x}) = 1 - P(Y=1 \;|\; \mathbf{x})$ . Esto nos da una probabilidad. Para la clase final, elegimos la etiqueta según $P(Y=1) > 0.5$ (u otro umbral). En el caso binario equivale a comparar si la salida lineal es mayor o menor que 0:
- Si $\mathbf{W}^T\mathbf{x} + b > 0$ , predice “1”.
- Si $\mathbf{W}^T\mathbf{x} + b < 0$ , predice “0” (o “-1”).
Conexión distancia-probabilidad
En modelos lineales clásicos (p.e., SVM), la salida $\mathbf{W}^T\mathbf{x} + b$ indica una distancia (o margen) respecto al hiperplano. Para convertir dicha cantidad en una probabilidad, aplicamos la función sigmoide, que comprime valores reales (infinitos en ambos extremos) a un rango de 0 a 1.
Caso Multiclase: Softmax
Para $C$ clases, generalizamos la función logística a softmax, asignando parámetros $\theta^{(1)}, \dots, \theta^{(C)}$ (un vector por clase) y obteniendo probabilidades que suman 1:
$$ P(Y = c) \;=\; \frac{\exp^{<\theta^{(c)} \mid \mathbf{X}>}} {\sum_{j=1}^{C} \exp^{<\theta^{(j)} \mid \mathbf{X}>}} \quad,\quad c=1,\dots,C. $$donde:
- $\theta^{(c)}$ son los parámetros asociados a la clase $c$ .
- La suma de probabilidades sobre las $C$ clases es igual a 1 (gracias al denominador).
La clase final se predice con la regla:
$$ \hat{c}(\mathbf{X}) \;=\; \arg\max_{1 \le c \le C} \,P(Y=c). $$Es habitual agrupar todos los vectores $\theta^{(c)}$ en una misma matriz:
$$ \theta \;=\; \begin{pmatrix} \vertbar & \vertbar & \cdots & \vertbar \\ \theta^{(1)} & \theta^{(2)} & \dots & \theta^{(C)} \\ \vertbar & \vertbar & \cdots & \vertbar \end{pmatrix}. $$(Cada columna es un vector de parámetros para la clase correspondiente.)
Uso de Scikit-learn
scikit-learn (sklearn) es una biblioteca de Python que nos permite entrenar y probar modelos de Machine Learning con funciones normalizadas.
Funciones generales
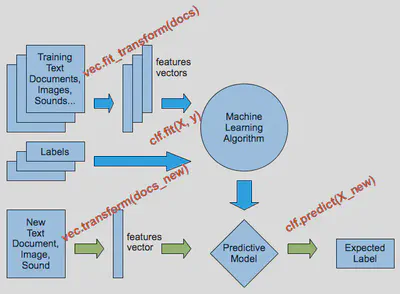
En sklearn:
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import SGDClassifier
data = load_iris()
X, y = data.data, data.target
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.4, random_state=0)
clf = SGDClassifier(max_iter=1000, tol=1e-3)
clf.fit(X_train, y_train)
print(clf.score(X_test, y_test))
(Para el orador: Subraya la facilidad de implementación y las funciones de utilidad para preprocesar, hacer feature extraction, validación cruzada, etc.)
Conjuntos de datos, extracción de características y preprocesamiento
- Múltiples datasets de juguete: Iris, Digits, Wine, etc.
- Conjuntos más grandes: RCV1 (texto), Faces (imágenes), etc.
- Módulos como
feature_extraction,feature_selection,preprocessingpara: - Vectorizar texto
- Seleccionar atributos relevantes
- Normalizar los datos
- Rellenar valores faltantes
(Para el orador: Invita a explorar la documentación sklearn.org y mostrar un ejemplo interactivo si hay tiempo.)
Validación cruzada y búsqueda de hiperparámetros
Incluye herramientas como:
train_test_splitKFold,StratifiedKFoldpara dividir los datoscross_val_scorepara evaluar un modelo en K particionesGridSearchCVoRandomizedSearchCVpara probar múltiples parámetros y hacer validación cruzada
from sklearn.model_selection import GridSearchCV
parameters = {'kernel':('linear','rbf'), 'C':[1,10]}
svc = svm.SVC(gamma="scale")
clf = GridSearchCV(svc, parameters, cv=5)
clf.fit(X, y)
(Para el orador: Resaltar la importancia de la validación cruzada para evitar sobreajustes y encontrar buenos hiperparámetros.)
Conclusión
En esta clase hemos visto:
- Cómo un clasificador lineal separa el espacio con un hiperplano.
- La regresión lineal como caso de modelo lineal para predicción de variables continuas.
- Cómo extender la linealidad introduciendo variables polinómicas o el truco del Bias.
- Un breve vistazo a la regresión logística, esencial para clasificación binaria y multi-clase con softmax.
- scikit-learn y sus funcionalidades para datasets, entrenamiento, validación y selección de hiperparámetros.
(Para el orador: concluye enfatizando que, aunque hay modelos más complejos como redes neuronales o ensembles, entender los modelos lineales es clave para la práctica de Machine Learning y la interpretación de resultados.)