Clustering

The slides are available here!

En aprendizaje no supervisado, no hay una variable objetivo \(Y\) etiquetada que queramos predecir. El objetivo es descubrir estructuras en los datos, como grupos (clusters), patrones o regularidades. Esto difiere del aprendizaje supervisado, donde sí conocemos las etiquetas \((\mathbf{X}_i, Y_i)\) y buscamos una función \(f\) que prediga \(Y\) a partir de \(\mathbf{X}\).

---

Clustering: Principio

¿Por qué clústeres?

• Topic modeling: agrupar documentos o comentarios según su tema.
• Análisis de sentimientos: reagrupar comentarios de usuarios para descubrir críticas comunes o elogios.
• Segmentación de clientes: en marketing, agrupar clientes con comportamientos similares.
• Eficiencia: entrenar submodelos especializados en cada clúster de datos.

Ambigüedad

Distintas particiones pueden ser igualmente válidas:

No siempre hay una sola respuesta a “cómo” agrupar.

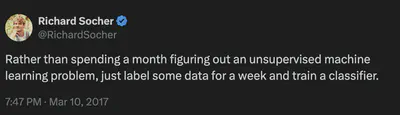
Objetivo intuitivo

Disminuir la distancia intra-cluster (los puntos de un mismo grupo están juntos) y aumentar la distancia inter-cluster (grupos lejos entre sí):

---

K-means

Idea general

Separar los datos en \(K\) grupos usando “centroides” (medias de cada clúster):

Minimizar la SSE (Sum of Squared Errors)

K-means particiona los datos \(\Xb_i\) en \(K\) clústeres \(\{\mathcal{C}_1,\dots,\mathcal{C}_K\}\) para minimizar:

\[ G(\mathcal{C}_1,\dots,\mathcal{C}_K) = \sum_{k=1}^K \sum_{i\in\mathcal{C}_k} \|\Xb_i - \mu_k\|^2, \]

donde \(\mu_k\) es el centroide del clúster \(k\). Cada punto se asigna al \(\mu_k\) más cercano en norma Euclídea.

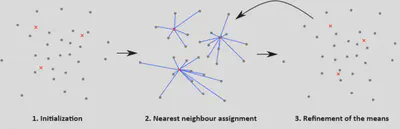
Algoritmo iterativo

1. Asignación: Conociendo los centroides \(\mu_k\), cada punto se asigna al más cercano.
2. Actualización: Conociendo la asignación, se recalculan los centroides \(\mu_k\) como la media de los puntos en cada clúster.
3. Se repite hasta que la inercia (SSE) deje de disminuir significativamente.

Dependencia de la inicialización

Es un problema no convexo, por lo que su solución depende de la semilla inicial:

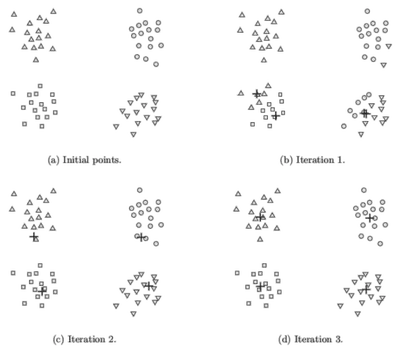
Solución: ejecutar K-means varias veces y elegir la partición con menor SSE.

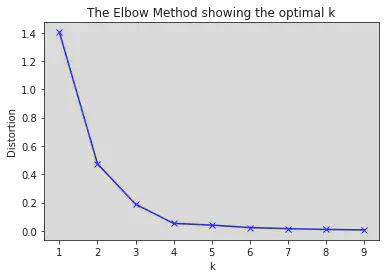
Elección de \(K\)

El número de clústeres debe fijarse antes. Se puede explorar varios valores y usar el método del codo (elbow method):

---

DBSCAN

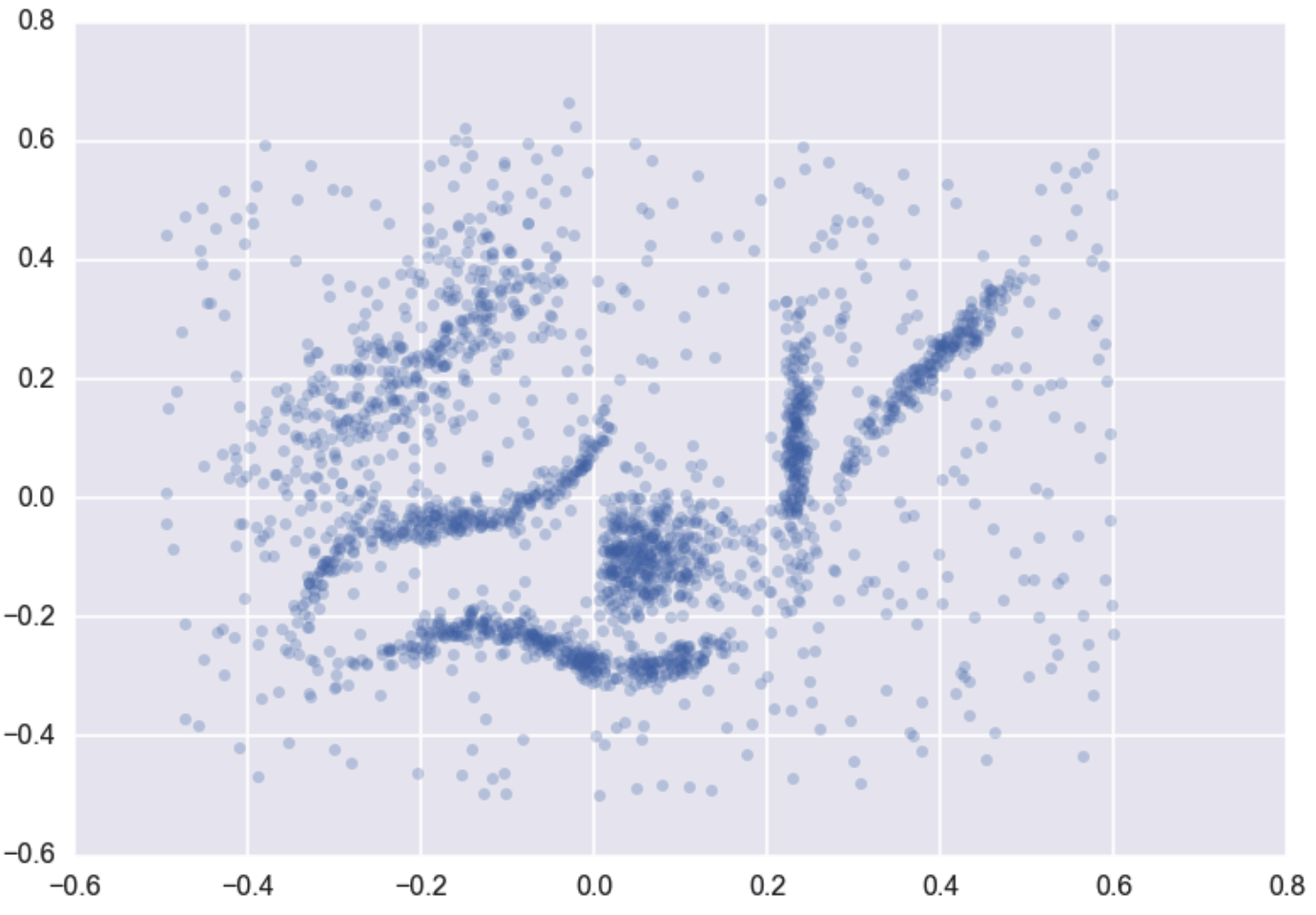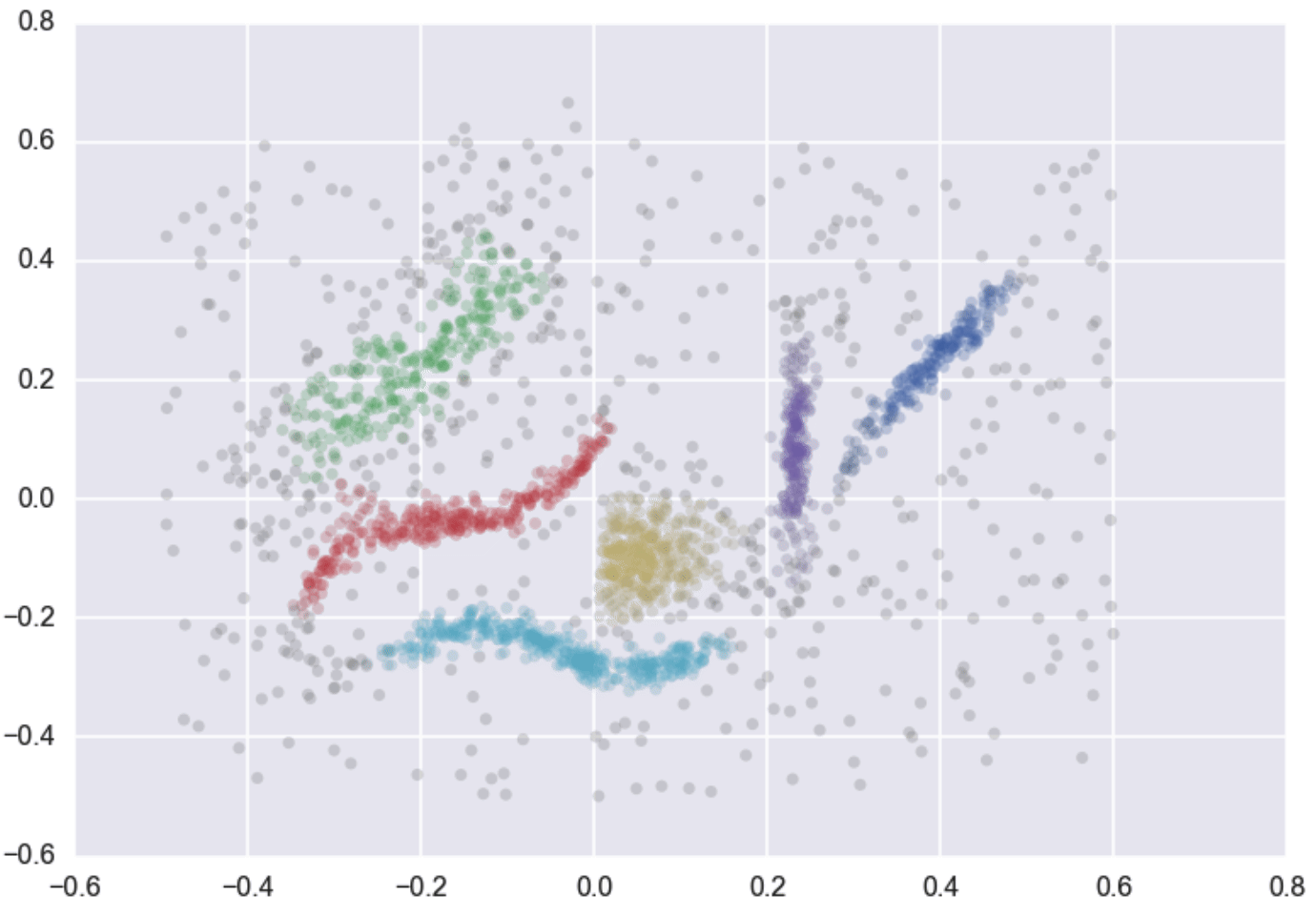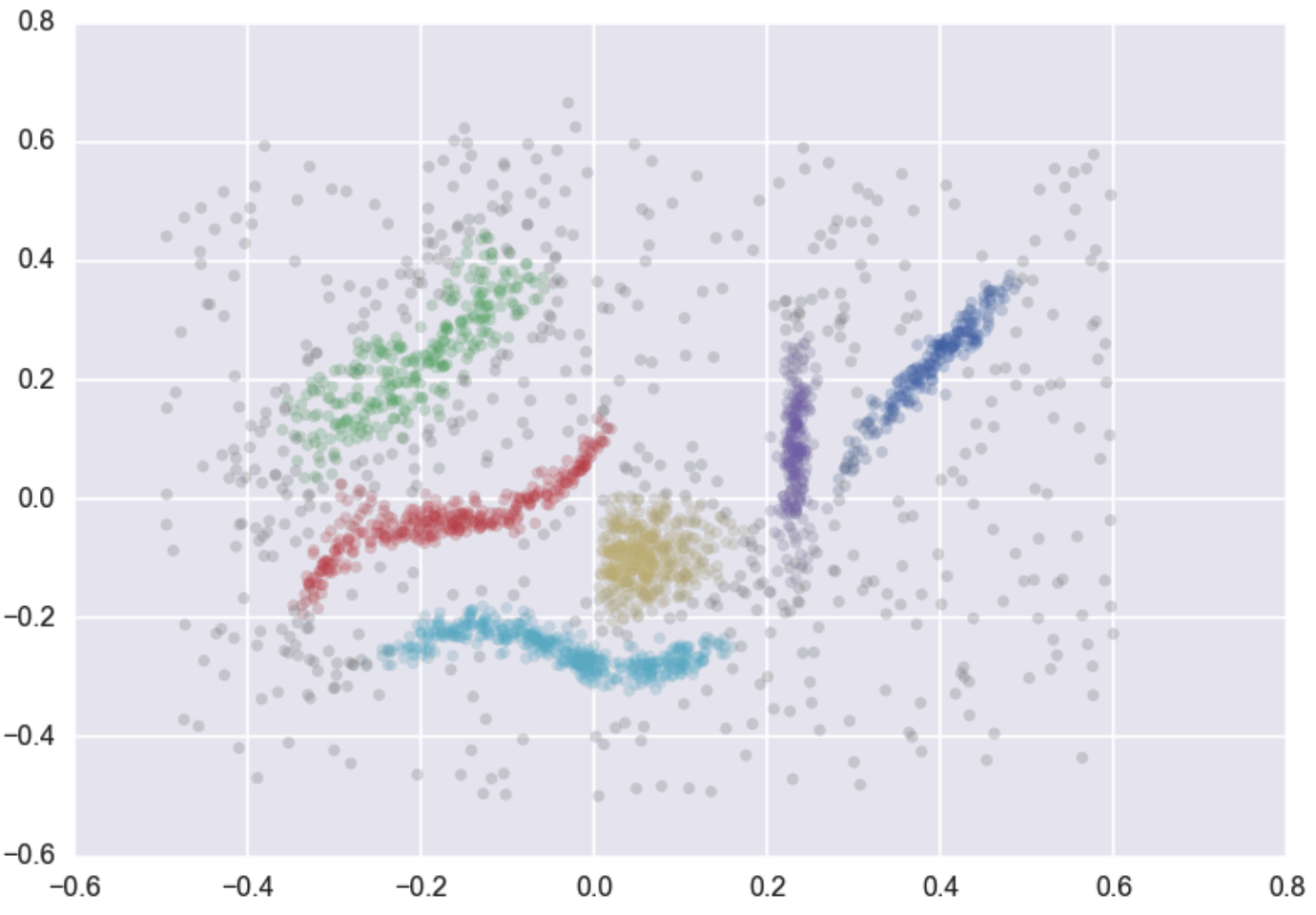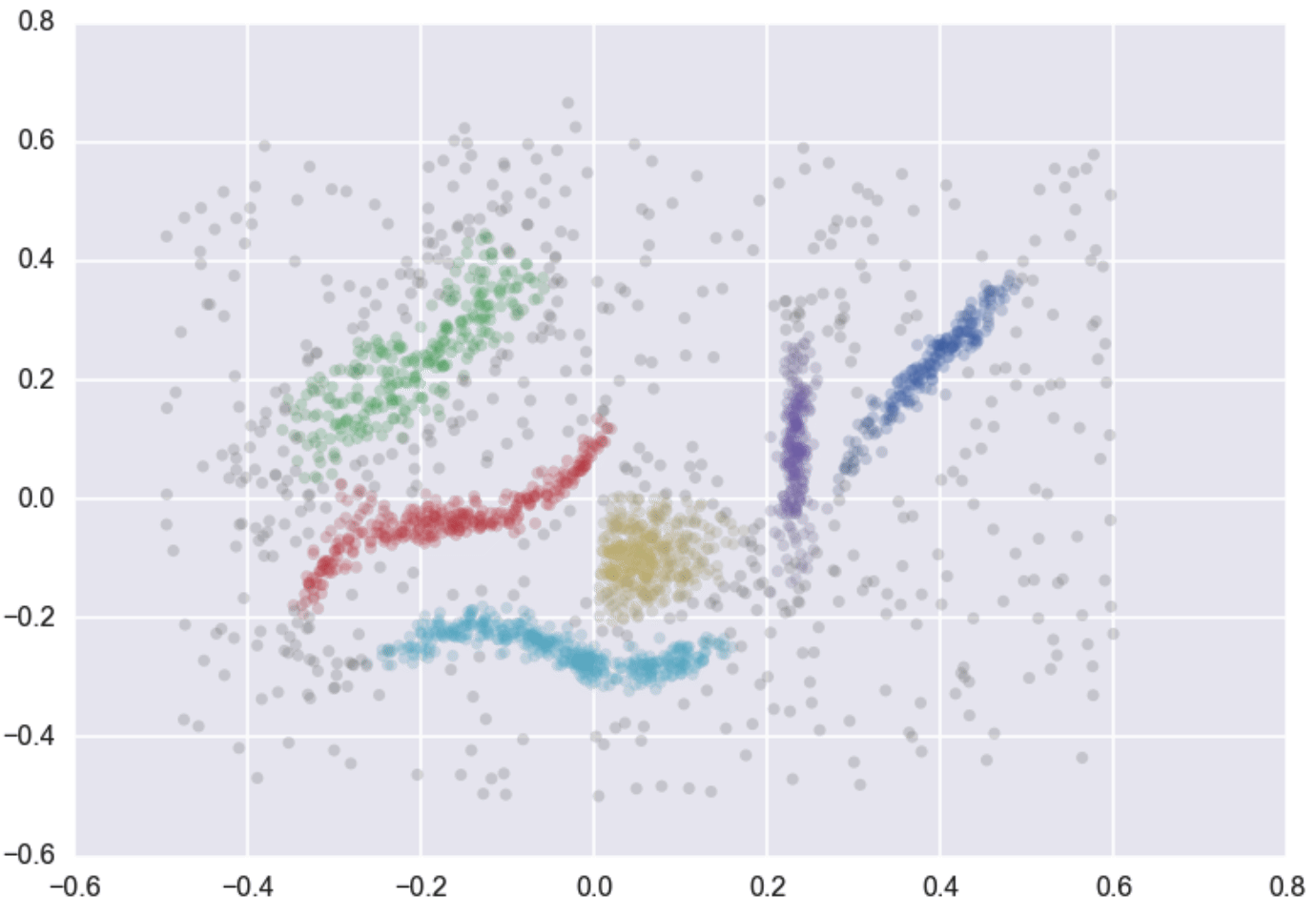
DBSCAN (Density-Based Spatial Clustering of Applications with Noise) busca regiones densas y marca los puntos dispersos como ruido.

Ejemplo

Principios

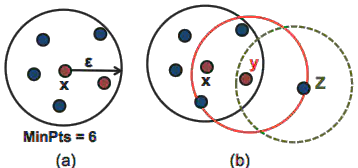
• Parámetros:
  • \(\texttt{eps} (\varepsilon)\): radio de vecindad.
  • \(\texttt{min\_samples}\): mínimo de puntos para que un punto sea núcleo (core).
• Clasifica en core, border, noise:
  • Core: al menos \(\texttt{min\_samples}\) puntos en su vecindad.
  • Border: no llega a ese umbral, pero está dentro del vecindario de un core.
  • Noise: no pertenece a core ni al vecindario de un core.

Ventajas y Desventajas

Ventajas:

• Detecta formas arbitrarias (no sólo esferas).
• Identifica outliers (ruido).
• Menos parámetros que métodos jerárquicos.

Desventajas:

• Sensible a \(\texttt{eps}\) y \(\texttt{min\_samples}\).
• Si la densidad varía drásticamente, un único \(\texttt{eps}\) no es apropiado.
• Difícil en alta dimensionalidad.

Elección de \(\texttt{minPts}\) y \(\varepsilon\)

• \(\texttt{minPts}\): regla de pulgar \(\texttt{minPts}\ge D+1\) (donde \(D\) = dimensión).
• \(\varepsilon\): usar gráfico de k-dist y buscar el “codo”.
• OPTICS es una alternativa más avanzada que ajusta la densidad de forma variable.

---

Clustering Jerárquico

Bisecting K-means

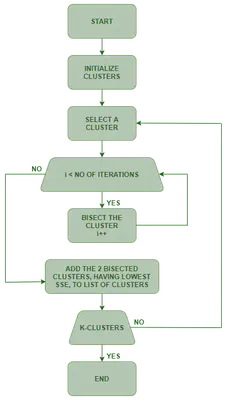
Bisecting K-means:

1. Arranca con todos los puntos como un clúster.
2. Aplica K-means con \(k=2\) (bisect) para dividirlo en 2.
3. Escoge el clúster con mayor SSE y lo subdivide.
4. Repite hasta lograr \(K\) clústeres.

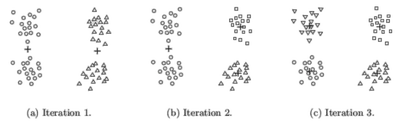
Ventajas: combinan jerarquía y rapidez de K-means.
Algoritmo:

---

Jerárquico Aglomerativo (HAC)

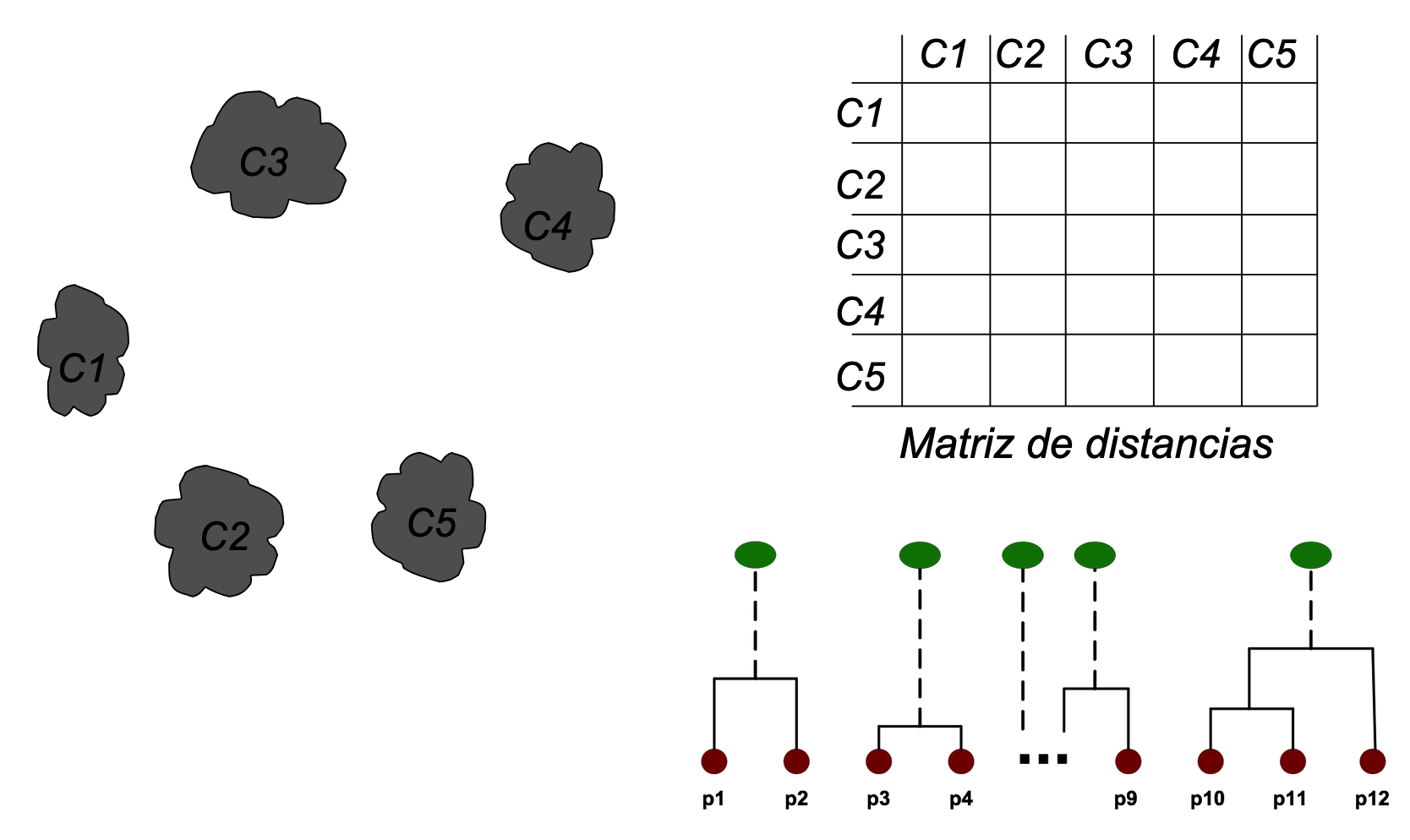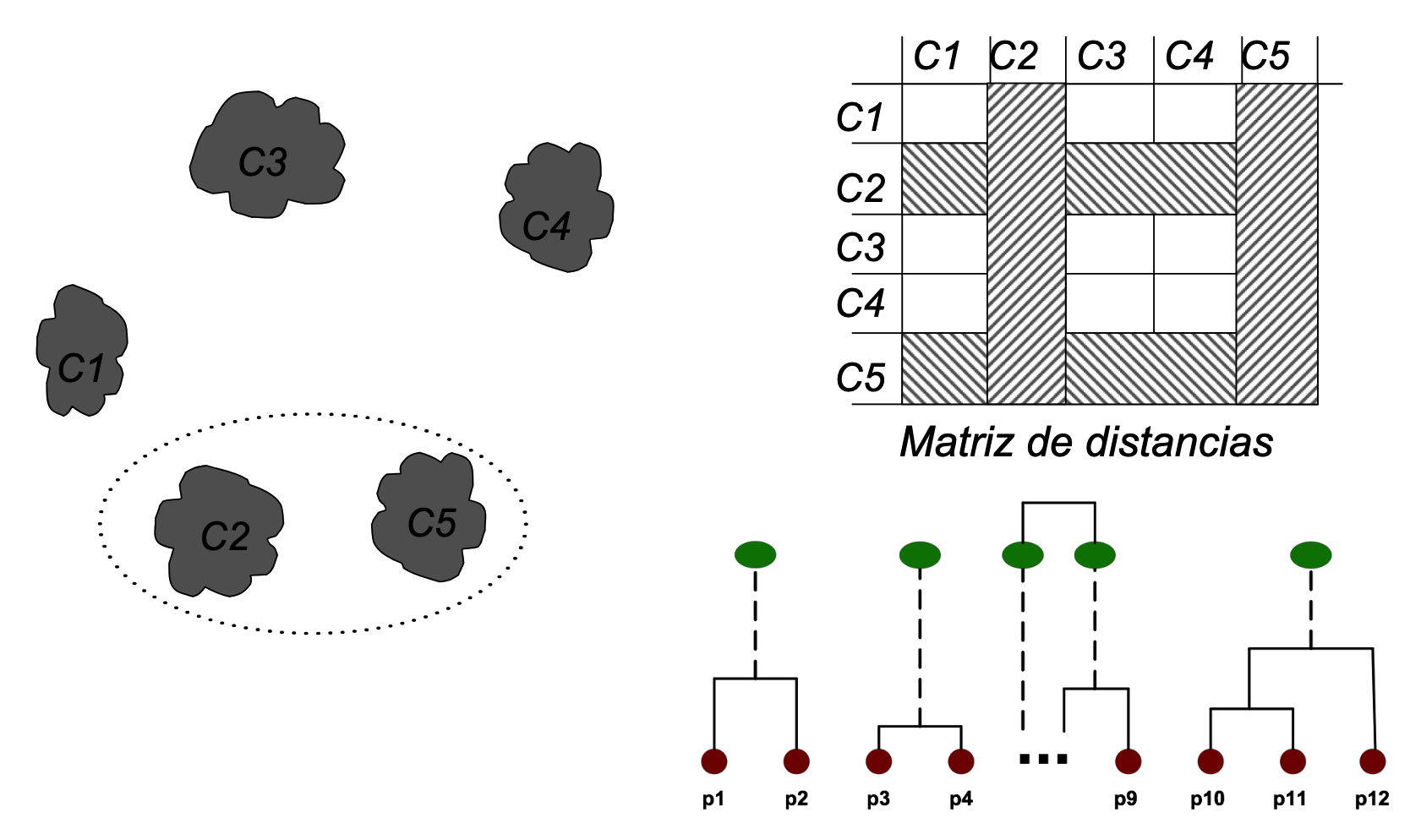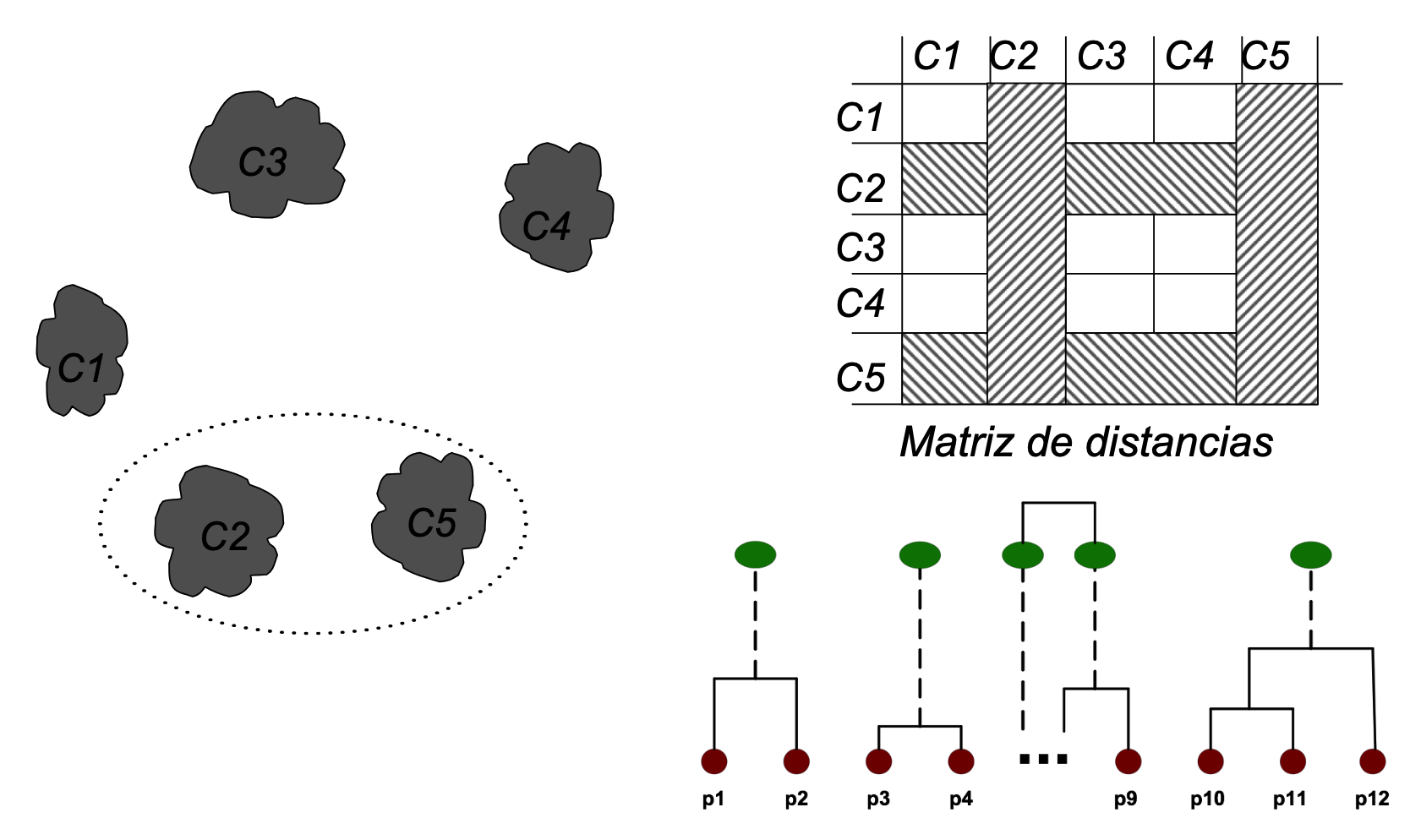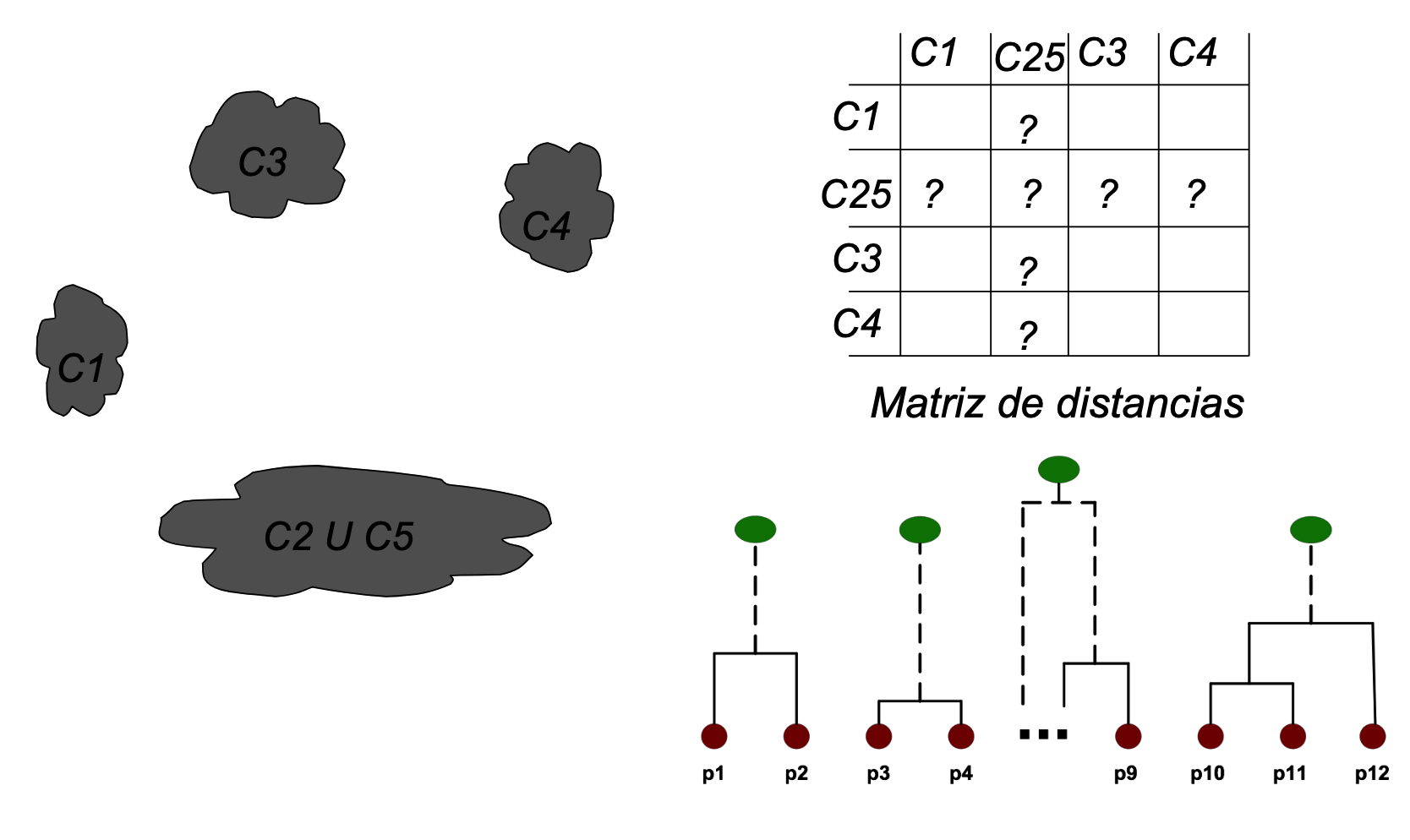
Otro enfoque jerárquico:

• Cada punto inicia como un clúster propio.
• Se fusionan iterativamente los 2 clústeres más cercanos.
• Se actualiza la distancia con el nuevo clúster.
• Hasta que quede un solo clúster.

Distancia entre clústeres (Linkage):

Se define la “distancia” entre dos grupos:

• Single linkage: menor distancia entre pares de puntos (sensibilidad al ruido).
• Complete linkage: mayor distancia entre pares de puntos.
• Average linkage: promedio de distancias entre pares (compromiso).
• Centroid linkage: distancia entre centroides.

---

HDBSCAN

HDBSCAN: extensión jerárquica de DBSCAN

• Explora múltiples densidades.
• No fija un único \(\varepsilon\).
• Elige subconjuntos estables dentro de la jerarquía de densidad.

Documentación HDBSCAN

---

Métricas de Validación

A diferencia del aprendizaje supervisado, muchas veces no hay etiquetas para evaluar la calidad de un clustering. Dos enfoques:

1. Métricas externas (hay etiquetas reales):
   • Homogeneidad, Completeness, V-measure.
   • Rand Index, Fowlkes–Mallows.
   • Mutual Information (MI).
2. Métricas internas (sólo datos y clústeres):
   • Silhouette (valores entre -1 y 1).
   • SSE (inercia en K-means).

Resumen rápido

• Homogeneidad: cada clúster contiene sólo puntos de una clase.
• Completeness: cada clase está contenida en un único clúster.
• V-measure: media armónica de las dos.
• Fowlkes–Mallows: ve pares de puntos coincidentes en la etiqueta y en el cluster.
• Silhouette: cohesión y separación sin usar clases reales.

---

Otros métodos de clustering

Existen varias alternativas según forma de los clústeres, ruido, densidad variable, etc.

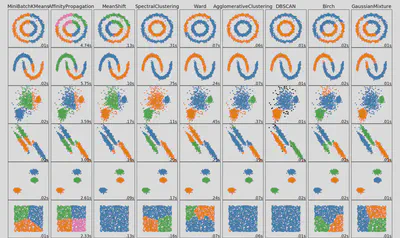
Tabla de referencia (Scikit-learn):

Method Name	Parameters	Scalability	Use Case	Geometry (Metric Used)
K-Means	Number of clusters	Very large n_samples, medium n_clusters with MiniBatch code	General-purpose, even cluster size, flat geometry, not too many clusters, inductive	Distances between points
Affinity Propagation	Damping, sample preference	Not scalable with n_samples	Many clusters, uneven cluster size, non-flat geometry, inductive	Graph distance (e.g., nearest-neighbor graph)
Mean-Shift	Bandwidth	Not scalable with n_samples	Many clusters, uneven cluster size, non-flat geometry, inductive	Distances between points
Spectral Clustering	Number of clusters	Medium n_samples, small n_clusters	Few clusters, even cluster size, non-flat geometry, transductive	Graph distance (e.g., nearest-neighbor graph)
Ward Hierarchical Clustering	Number of clusters or distance threshold	Large n_samples and n_clusters	Many clusters, possibly connectivity constraints, transductive	Distances between points
Agglomerative Clustering	Number of clusters or distance threshold, linkage type, distance	Large n_samples and n_clusters	Many clusters, possibly connectivity constraints, non-Euclidean distances, transductive	Any pairwise distance
DBSCAN	Neighborhood size	Very large n_samples, medium n_clusters	Non-flat geometry, uneven cluster sizes, outlier removal, transductive	Distances between nearest points
HDBSCAN	Minimum cluster membership, minimum point neighbors	Large n_samples, medium n_clusters	Non-flat geometry, uneven cluster sizes, outlier removal, transductive, hierarchical, variable cluster density	Distances between nearest points
OPTICS	Minimum cluster membership	Very large n_samples, large n_clusters	Non-flat geometry, uneven cluster sizes, variable cluster density, outlier removal, transductive	Distances between points
Gaussian Mixtures	Many	Not scalable	Flat geometry, good for density estimation, inductive	Mahalanobis distances to centers
BIRCH	Branching factor, threshold, optional global clusterer	Large n_clusters and n_samples	Large dataset, outlier removal, data reduction, inductive	Euclidean distance between points
Bisecting K-Means	Number of clusters	Very large n_samples, medium n_clusters	General-purpose, even cluster size, flat geometry, no empty clusters, inductive, hierarchical	Distances between points

Más info en: clustering scikit-learn docs

---

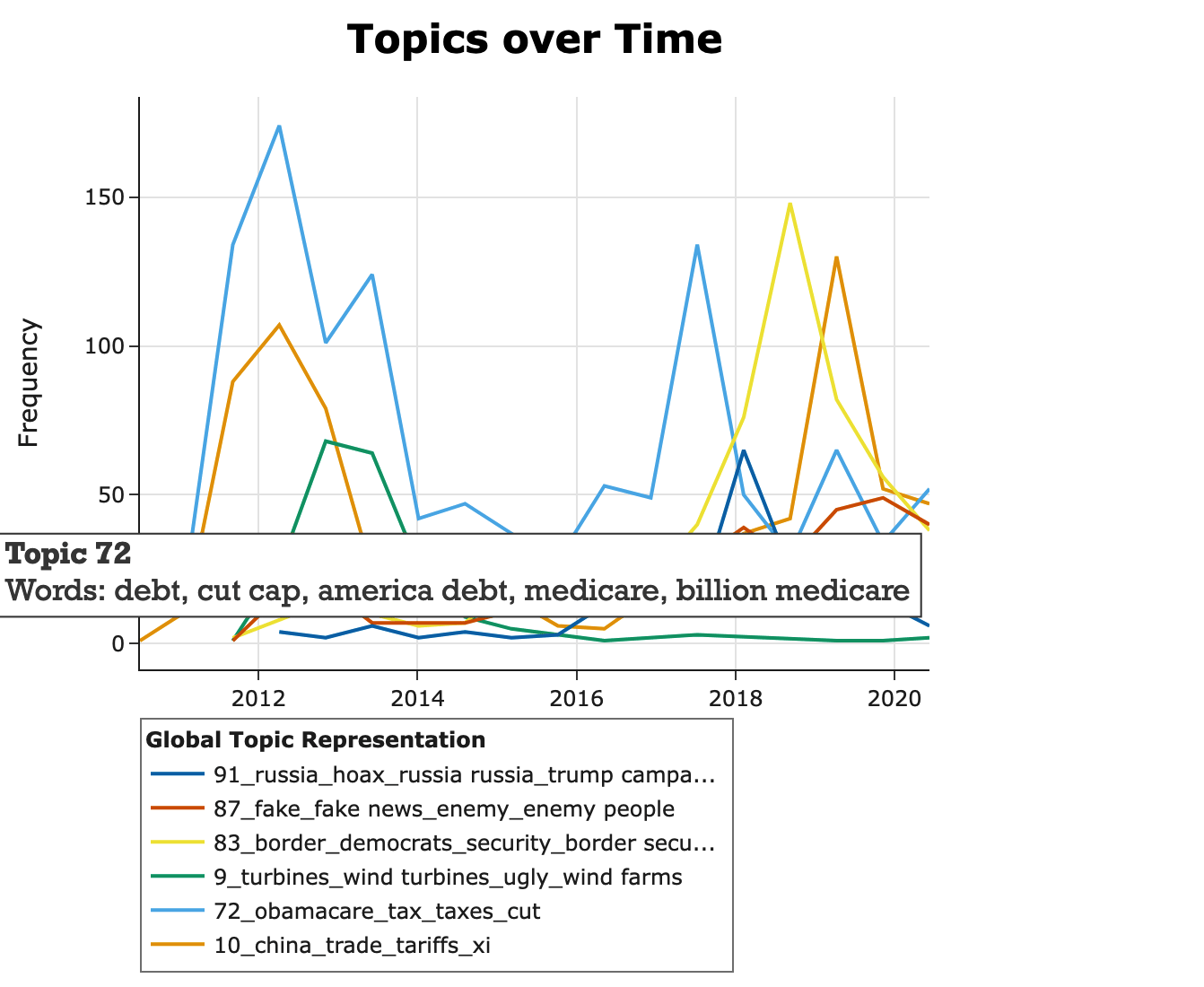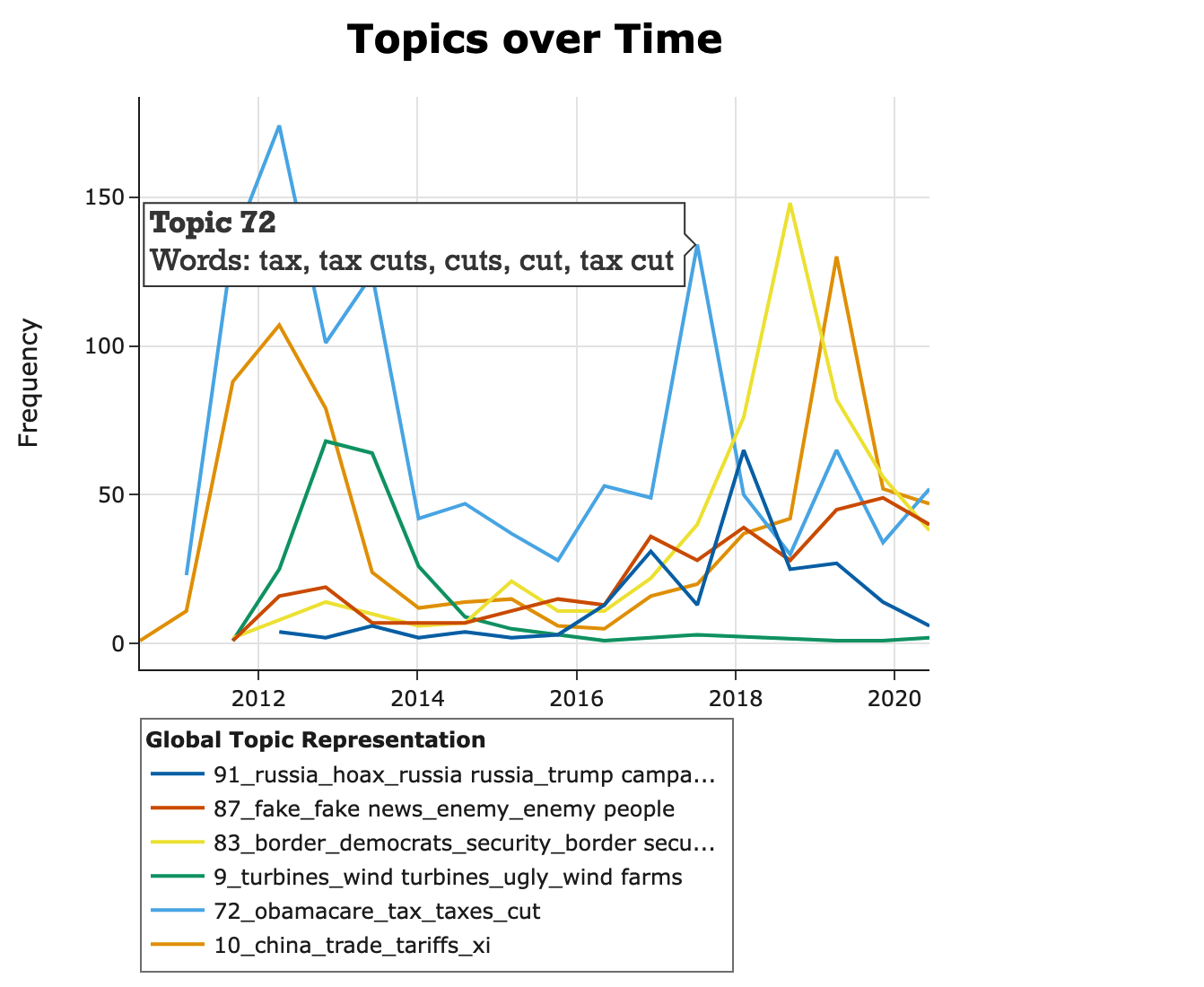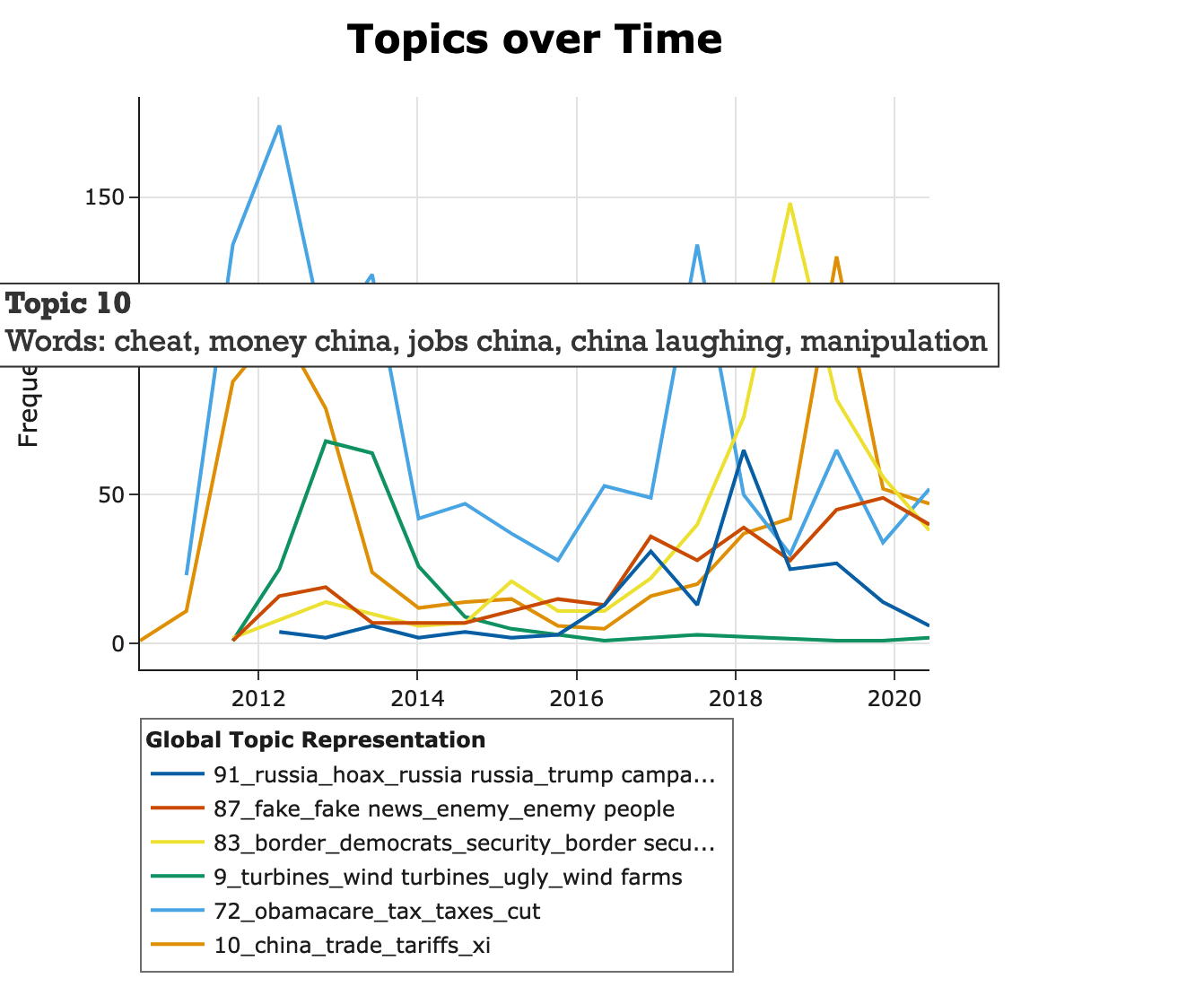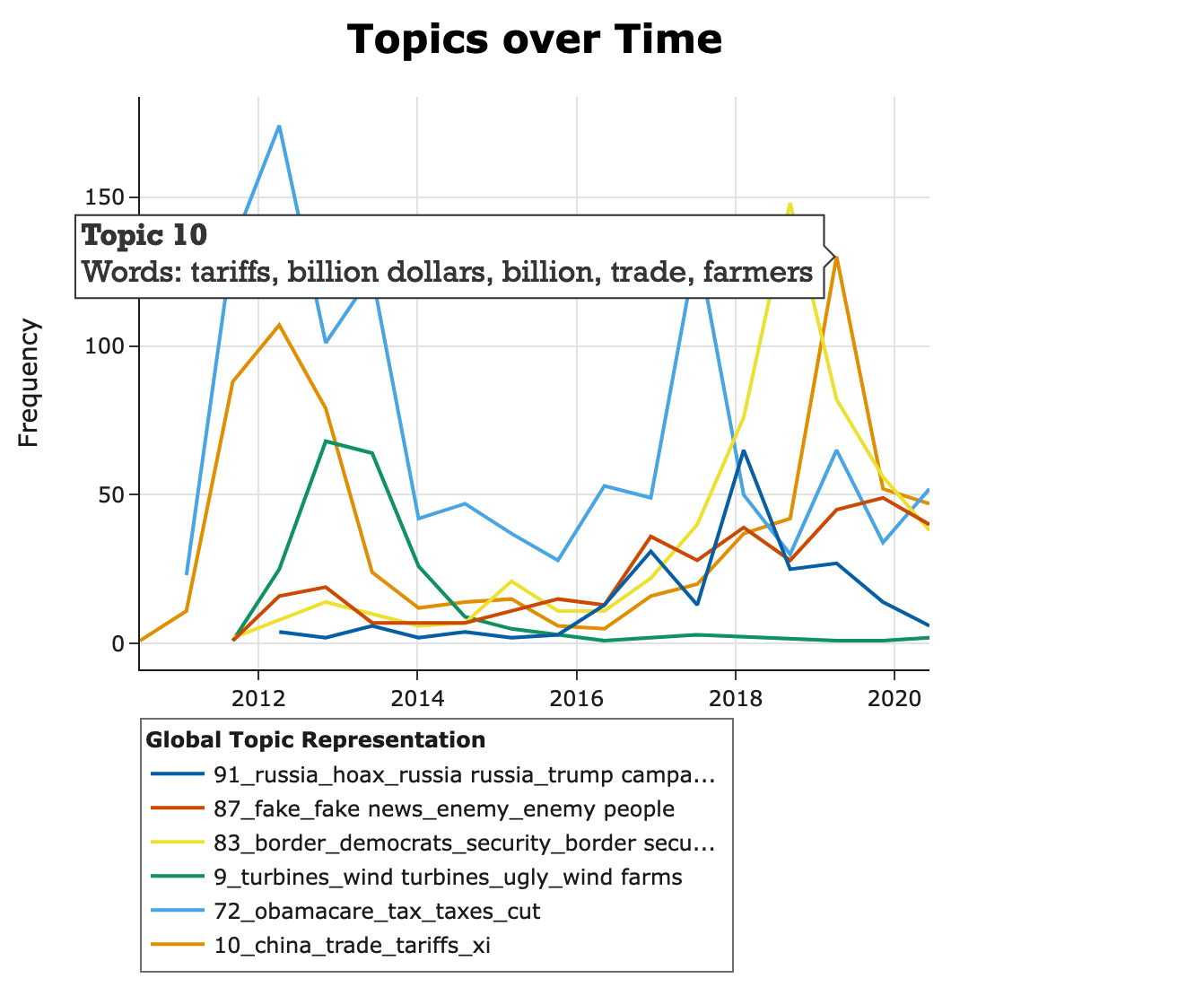
Use-case: BERTopic

BERTopic es una librería que combina embeddings (BERT) + clustering para topic modeling sobre textos.

Puede:

• Agrupar oraciones/documentos en “temas” usando embeddings.
• Visualizar la evolución de temas en el tiempo (dynamic topic modeling).
• Hacer clustering jerárquico en temas descubiertos.

BERTopic docs

---

See you in the classroom!