SVM
The slides are available here!
Máquinas de Vectores de Soporte (SVM)
Las Máquinas de Vectores de Soporte son modelos de clasificación (o regresión) que buscan encontrar un hiperplano o frontera de decisión que maximice el margen entre las clases. A continuación, veremos sus conceptos clave, la formulación lineal, el uso de kernels y, finalmente, la extensión a la regresión (SVR).
Separadores de Gran Margen
El objetivo de las SVM es encontrar un separador (en dimensión \(d\), un hiperplano) que no solo divida correctamente las clases, sino que lo haga maximizando la distancia mínima con cualquier punto de entrenamiento.
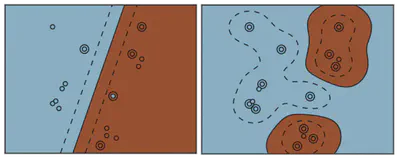
En casos lineales y perfectamente separables, puede haber varios hiperplanos que distingan las clases. La pregunta es: ¿Cuál elegir?
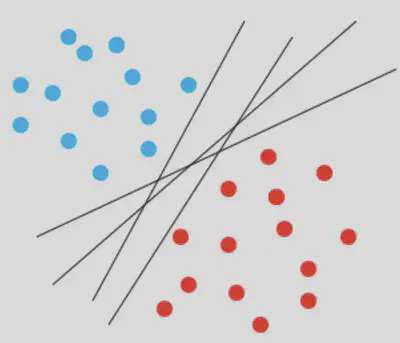
La SVM opta por el que maximiza el margen, buscando así una mejor capacidad de generalización.
Clasificador lineal: recordatorio
Un clasificador lineal en \(\mathbb{R}^d\) se define por:
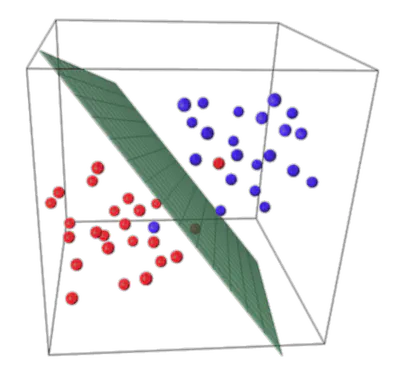
\[ f(\mathbf{X}) = \mathrm{signo}(\mathbf{W}^\top \mathbf{X} + b). \]En la siguiente figura se ilustra una separación lineal (en 3D) que se proyecta a una separación curva al volver al espacio 2D:
SVM lineal: márgenes y restricción de separabilidad
El hiperplano \(\mathbf{W}^\top \mathbf{X} + b = 0\) y los planos paralelos \(\mathbf{W}^\top \mathbf{X} + b = \pm 1\) marcan el margen. Cuanto mayor sea la distancia entre esos planos, mayor será la robustez.
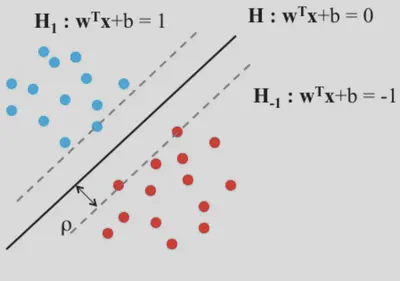
Margen geométrico: Consideremos los planos de decisión \(\mathbf{W}^\top \mathbf{X} + b = \pm 1\). La distancia entre esos dos planos es:
\[ \frac{2}{\|\mathbf{W}\|}. \]Por ello, maximizar esa distancia es equivalente a minimizar \(\|\mathbf{W}\|\).
Forma habitual en SVM:
Para comodidad numérica, se minimiza \(\tfrac{1}{2}\|\mathbf{W}\|^2\) en lugar de \(\|\mathbf{W}\|\), pero el criterio es el mismo.
Para datos (casi) separables, la SVM busca:
\[ \begin{aligned} & \min_{\mathbf{W}, b} \quad \frac{1}{2}\|\mathbf{W}\|^2 \\ & \text{sujeto a } \quad Y_i \, (\mathbf{W}^\top \mathbf{X}_i + b)\; \ge 1,\quad \forall i. \end{aligned} \]En suma, la restricción \(Y_i(\mathbf{W}^\top \mathbf{X}_i + b)\ge 1\) asegura que cada punto esté al menos a distancia \(1/\|\mathbf{W}\|\) del hiperplano, y al reducir \(\|\mathbf{W}\|\) aumentamos este margen.
Formulación primal y dual
Los problemas primal y dual son equivalentes en entornos convexos.
El problema Primal:
\[ \begin{aligned} &\min \quad z = c^t x, \\ &\text{subject to} \quad A x \ge b, \\ &\qquad\quad\;\; x \ge 0. \end{aligned} \]El problema Dual:
\[ \begin{aligned} &\max \quad z = b^t y, \\ &\text{subject to} \quad A^t y \le c, \\ &\qquad\quad\;\; y \ge 0, \end{aligned} \]En la práctica se implementan algoritmos para el problema dual, sobre todo cuando se utilizan kernels.
Para resolverlo, se introduce el Lagrangiano y se pasa a la formulación dual. De este modo:
- Primal: parámetros \(\mathbf{W}, b\).
- Dual: multiplicadores \(\alpha_i\).
Introducción del Lagrangiano y condiciones KKT
Para resolver el problema de optimización con restricciones
\[ \min_{\mathbf{W},b} \quad \frac{1}{2}\|\mathbf{W}\|^2 \quad\text{sujeto a}\quad Y_i(\mathbf{W}^\top\mathbf{X}_i + b)\;\ge\;1, \]se introduce el Lagrangiano:
\[ \mathcal{L}(\mathbf{W}, b, \boldsymbol{\alpha}) \;=\; \tfrac{1}{2}\|\mathbf{W}\|^2 \;-\; \sum_{i=1}^n \alpha_i \,\bigl(Y_i(\mathbf{W}^\top \mathbf{X}_i + b) - 1\bigr), \]donde \(\alpha_i \ge 0\) son los multiplicadores de Lagrange.
Las Condiciones de Karush-Kuhn-Tucker (KKT) aplicadas a este problema especifican, entre otras, que:
- \(\nabla_{\mathbf{W}} \,\mathcal{L} = 0\) y \(\nabla_b \,\mathcal{L} = 0\) (estacionaridad).
- \(\alpha_i \ge 0\).
- \(\alpha_i \,\bigl[Y_i(\mathbf{W}^\top \mathbf{X}_i + b)-1\bigr] = 0\) (complementariedad):
esto implica que para cada \(i\), o bien la restricción se cumple con margen (estricto) o \(\alpha_i=0\).
Resolviendo el problema Dual y aparición de \(\alpha_i\)
- Construcción del Dual:
Se reemplaza \(\|\mathbf{W}\|^2\) y se resuelve en función de \(\boldsymbol{\alpha}\). El problema dual pasa a ser: \[ \begin{aligned} &\max_{\boldsymbol{\alpha}} \quad \sum_{i=1}^n \alpha_i \;-\; \tfrac{1}{2}\sum_{i,j} \alpha_i \alpha_j \,Y_i Y_j \,\langle \mathbf{X}_i,\mathbf{X}_j\rangle,\\ &\text{sujeto a}\quad \alpha_i \ge 0,\;\; \sum_{i=1}^n \alpha_i Y_i = 0. \end{aligned} \] - Solución para \(\mathbf{W}\):
De las KKT, se deduce que \[ \mathbf{W} \;=\; \sum_{i=1}^n \alpha_i \,Y_i \,\mathbf{X}_i. \] - Clasificador:
\[ f(\mathbf{X}) \;=\; \mathrm{signo}\!\Bigl(\sum_{i=1}^n \alpha_i\,Y_i\,\langle\mathbf{X}_i,\mathbf{X}\rangle + b \Bigr). \]
Notar que en este punto aún no hemos introducido el concepto de soft margin. Cuando todos los datos son separables y no hay ruido, cada punto cumple la restricción sin violarla. Una vez introducidos errores o ruido, pasaremos a la versión soft margin. mal-dual (izq/primal, der/dual)](figures/dual.png “Un problema Dual”)
Vectores de Soporte
Tras la optimización, el hiperplano se expresa como:
\[ \mathbf{W} = \sum_{i=1}^{n} \alpha_i \, Y_i \, \mathbf{X}_i \]y la decisión:
\[ f(\mathbf{X}) = \mathrm{signo}\!\Big(\sum_{i=1}^{n} \alpha_i \,Y_i\;\langle \mathbf{X}_i,\mathbf{X}\rangle + b\Big). \]Solo los puntos con \(\alpha_i \neq 0\) se llaman vectores de soporte, aquellos que “soportan” el margen.
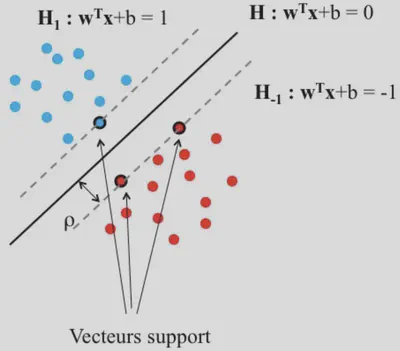
Soft margin y ruido
Cuando hay ruido, el plan optimal no es necesariamente el mejor: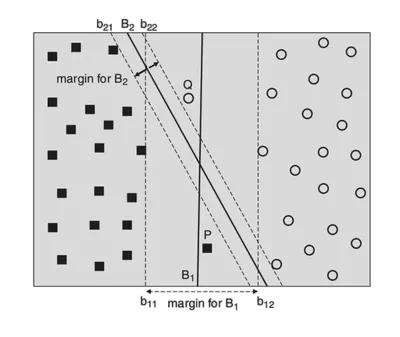
Cuando los datos no son perfectamente separables (o hay ruido), se permiten variables de holgura \(\xi_i \ge 0\). Esto penaliza los errores o los puntos dentro del margen:
\[ \begin{aligned} & \min_{\mathbf{W},b} \quad \frac{1}{2}\|\mathbf{W}\|^2 + C \sum_{i}\xi_i \\ & \text{sujeto a} \quad Y_i(\mathbf{W}^\top \mathbf{X}_i + b) \ge 1 - \xi_i,\quad \xi_i \ge 0. \end{aligned} \]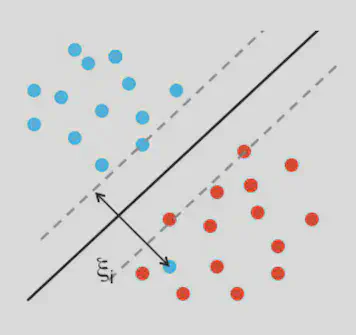
El parámetro \(C\) balancea la complejidad vs. el número de errores, y es un parametro de regularizacion.
Resolución Dual con KKT
Tras introducir variables de holgura \(\xi_i \ge 0\), la formulación primal se convierte en:
\[ \begin{aligned} & \min_{\mathbf{W}, b, \{\xi_i\}} \quad \frac{1}{2}\|\mathbf{W}\|^2 + C\sum_{i=1}^n \xi_i, \\ & \text{sujeto a} \quad Y_i(\mathbf{W}^\top\mathbf{X}_i + b)\;\ge\;1 - \xi_i,\quad \xi_i \ge 0. \end{aligned} \]En el Lagrangiano, aparecen ahora multiplicadores \(\alpha_i\) y \(\mu_i\) para manejar las restricciones asociadas a \(\xi_i\). Se obtienen condiciones KKT adicionales, incluyendo
\[ \alpha_i \,\bigl[Y_i(\mathbf{W}^\top\mathbf{X}_i + b)-1+\xi_i\bigr] \;=\; 0,\quad \mu_i\,\xi_i \;=\; 0,\quad 0 \;\le\;\alpha_i \;\le\; C. \]El problema dual final para la SVM con soft margin vuelve a ser:
\[ \begin{aligned} & \max_{\boldsymbol{\alpha}} \quad \sum_{i=1}^n \alpha_i \;-\; \tfrac{1}{2}\sum_{i,j} \alpha_i \alpha_j \,Y_i Y_j \,\langle \mathbf{X}_i,\mathbf{X}_j\rangle,\\ & \text{sujeto a} \quad 0 \;\le\;\alpha_i \;\le\; C,\quad \sum_{i=1}^n \alpha_i Y_i = 0. \end{aligned} \]Aquí, los puntos para los que \(\alpha_i\) está en el rango \((0, C)\) se convierten en los vectores de soporte, y la resolución sigue análoga al caso separable.
Equivalente de regularización (Hinge loss)
Otra forma de ver la SVM lineal es como un caso especial de pérdida bisagra (hinge loss) con regularización en la norma de \(\mathbf{W}\).
En el espacio primal, la minimización se puede escribir como:
donde \(\lambda\) es un parámetro de regularización relacionado inversamente con \(C\).
La pérdida (bisagra) \(\max(0,\,1 - Y_i(\mathbf{W}^\top \mathbf{X}_i + b))\) fuerza cada ejemplo a estar, idealmente, al menos a 1 de distancia del hiperplano, y penaliza las violaciones a ese margen. Así, minimizar la norma de \(\mathbf{W}\) y el costo bisagra conduce al mismo criterio de “gran margen” que describimos antes.
Kernel Trick y espacio aumentado
La separación lineal puede no ser posible en el espacio original, pero sí en una dimensión mayor. Aun así, no es necesario calcular explícitamente dicha transformación \(\varphi(\mathbf{X})\). El truco del kernel nos dice que:
\[ k(\mathbf{X},\mathbf{X}') = \langle \varphi(\mathbf{X}), \,\varphi(\mathbf{X}') \rangle. \]Aumento del espacio (idea)
En el nuevo espacio, la separación lineal puede existir aunque en el original no:
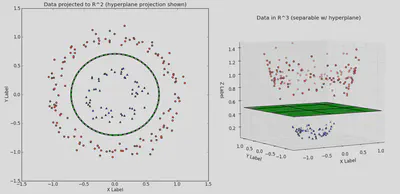
(Cuidado con la alta dimensionalidad si \(d\) es muy grande.)
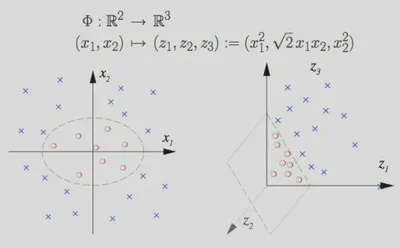
Ejemplo de Kernel Trick
Supongamos que queremos clasificar datos en \(\mathbb{R}^2\) usando un núcleo polinomial de grado 2. Podemos definir una transformación explícita:
\[ \varphi: (x_1,x_2) \;\mapsto\; (\,x_1^2,\;\sqrt{2}\,x_1x_2,\;x_2^2,\;\sqrt{2}\,x_1,\;\sqrt{2}\,x_2,\;1\,). \]Al calcular el producto punto en este espacio, se observa que:
\[ \langle \varphi(\mathbf{X}),\varphi(\mathbf{X}')\rangle \;=\; \bigl(\langle \mathbf{X},\mathbf{X}'\rangle + 1\bigr)^2 \]De modo que el kernel asociado es:
\[ k(\mathbf{X},\mathbf{X}') \;=\; \bigl( \mathbf{X}\cdot\mathbf{X}' + 1 \bigr)^2. \]Esto permite a la SVM trabajar implícitamente con una dimensión más alta sin calcular \(\varphi(\mathbf{X})\) ni \(\varphi(\mathbf{X}')\) de forma explícita.
Tipos de kernel comunes
Lineal
\[ k(\mathbf{X},\mathbf{X}') \;=\; \langle \mathbf{X},\;\mathbf{X}' \rangle \]Polinomial
\[ k(\mathbf{X},\mathbf{X}') \;=\; \bigl(\langle \mathbf{X}, \mathbf{X}' \rangle + c\bigr)^{d} \]Gaussiano (RBF)
\[ k(\mathbf{X},\mathbf{X}') \;=\; \exp\!\bigl(-\gamma\,\|\mathbf{X}-\mathbf{X}'\|^2\bigr) \]
Lineal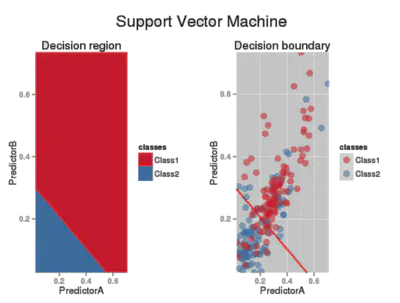
Polinomial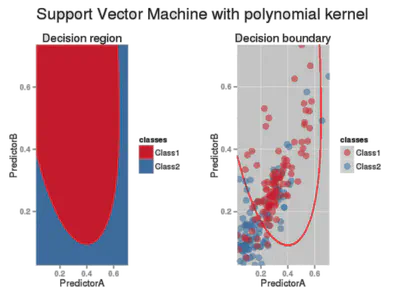
Gaussiano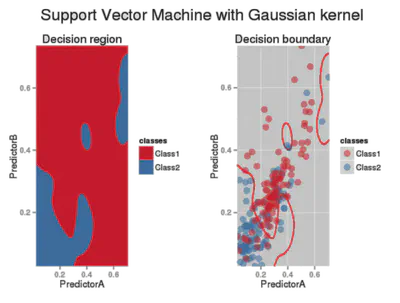
Conclusión de SVM
- Se basa en maximizar el margen (reduce sobreajuste).
- La solución surge de un problema de optimización convexa que se puede abordar en su versión dual.
- Los vectores de soporte son los únicos puntos relevantes para la frontera de decisión.
- Permite kernels para manejar no linealidades.
- Ajustar hiperparámetros (ej. \(C\), grado del polinomio, \(\gamma\) en el gaussiano) puede ser costoso.
Support Vector Regressor (SVR)
La SVM también puede adaptarse a tareas de regresión. En vez de separar puntos en clases, se busca que la predicción \(\hat{y}\) caiga en un tubo de ancho \(\epsilon\) en torno al valor real \(y\). A esto se lo denomina pérdida \(\epsilon\)-insensible.
Principio
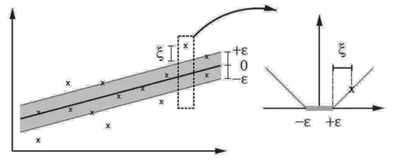
Si \(|\hat{y} - y| \leq \epsilon\), no se incurre en penalización. Caso contrario, se agregan variables \(\xi_i, \xi_i^*\) que miden el exceso del error respecto de \(\epsilon\).
Formulación
Primal para SVR:
\[ \min_{\mathbf{W},b} \;\; \tfrac{1}{2}\|\mathbf{W}\|^2 + C\sum_i (\xi_i + \xi_i^*) \]sujeto a
\[ \begin{cases} y_i - f(\mathbf{X}_i) \;\le\; \epsilon + \xi_i, \\ f(\mathbf{X}_i) - y_i \;\le\; \epsilon + \xi_i^*, \\ \xi_i,\xi_i^*\ge0. \end{cases} \]Dual: se obtienen multiplicadores \(\alpha_i,\alpha_i^*\) y la solución final es
\[ f(\mathbf{X}) \;=\; \sum_{i=1}^{n} (\alpha_i - \alpha_i^*)\,k(\mathbf{X}_i,\mathbf{X})\;+\;b. \]
Ejemplo
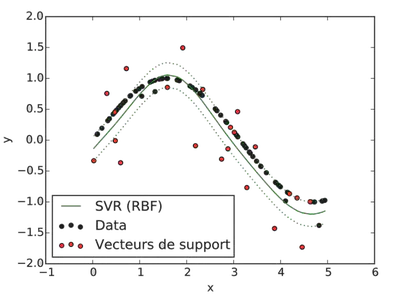
Solo los puntos que quedan fuera del tubo (por encima de \(\epsilon\)) se convierten en vectores de soporte.
Resumen SVR
- Extiende la SVM a regresión, usando la idea de máximo margen alrededor de la curva aprendida.
- El parámetro \(\epsilon\) controla el ancho de la zona “sin costo”; \(\xi_i,\xi_i^*\) miden el exceso.
- \(C\) regula la penalización por exceder \(\epsilon\).
- Se pueden usar kernels para la parte no lineal, igual que en la clasificación.
¡Eso es todo sobre SVM y SVR! Son métodos muy potentes y ampliamente utilizados en Machine Learning:
- SVM para clasificación binaria (y extensiones a multiclase).
- SVR para regresión con márgenes.
- Kernels para no linealidad en ambos casos.