Intro Aprendizaje Supervisado

The slides are available here!

Esta clase es bastante interesante ya que descubriran las bases del conocimiento utilizado para construir Machine Learning, Deep Learning e Inteligencia Artificial en general: Aprendizaje Supervisado!

Se trata de un entorno sencillo en el que un modelo aprenderá sus propios parámetros utilizando ejemplos y etiquetas asociadas. Revisaremos todos los conceptos importantes del aprendizaje supervisado, que son muy útiles para cualquiera que quiera trabajar como data scientist.

Generalidades

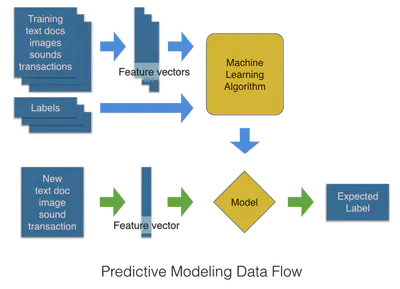
El aprendizaje supervisado utiliza datos y etiquetas para aprender a un modelo a reconocer padrones:

• Es necesario de transformar los documentos en vectores, para poder hacer la optimizacion
• El modelo va a apprender sus parametros sobre un conjunto de entrenamiento
• El modelo entrenado puede ser usado para predicir la etiquetas de nuevos datos que nunca ha visto antes
• El documento puede ser cualquier dato: audio, texto, imagen, video, usuario, red,…

Features y etiquetas

Se puede representar en un espacio los documentos como vectores. Aca cada punto es una cancion, que esta representando con su intensidad y tempo promedios. La etiqueta es la color del punto. Aca tenemos una tarea de clasificacion binaria de musica, segundo las preferencias de un usuario.

El objetivo del juego, va a ser de encontrar una funcion que separa el espacio en dos partes. Una donde hay las canciones que le gustan a la persona, y la otra parte que no le gustan. De este manera, cuando vamos a tener un nuevo punto en este espacio, podemos decir si la persona va a gustar o no esta cancion, lo que sea predicir su etiqueta!

En resumen

Se necesitan varias cosas para un entrenamiento

1. Tener datos etiquetados

• Conjunto de datos de tamaño $n$ , $\mathcal{D}_n = \{(\text{Doc}_i, Y_i), i=1..n\}$
• $\text{Doc}$ es una muestra (por ejemplo: una persona)
• $Y$ son las etiquetas (por ejemplo: monto del préstamo concedido)

2. Extraer los descriptores = transformar documentos en vectores

• $\mathbf{X}$ es un vector de observaciones (por ejemplo: edad, sexo, salario)
• $Y$ son las etiquetas (por ejemplo: monto del préstamo concedido)

3. Crear un modelo matemático $f_\theta$

• Modelo $f_\theta$ tal que $f_\theta(\mathbf{X})$ esté cerca de $Y$ (para regresión)
• $\theta$ es el conjunto de parámetros del modelo matemático

4. Implementar una función de costo (error) $\ell$ a minimizar

• Cuanto más se equivoque el modelo, mayor será el costo
• En general, se desea tener un costo pequeño

5. Encontrar los parámetros $\theta^*$ de manera que $\ell(f_{\theta^*}(\mathbf{X}_i), Y_i)$ sea pequeño

6. Probar $f_{\theta^*}$ en nuevos datos con una métrica de evaluación adecuada

Aprendizaje

Hay varios conceptos en el aprendizaje:

• Datos etiquetados: Regresión o Clasificación
• Extracción de características: Tono, Intensidad, Tempo o Edad, Salario, Género, etc.
• Modelo $f_\theta$: SVM, Regresión Logística, Bosque Aleatorio, CNN
• Función de costo a optimizar: Pérdida de Bisagra, Pérdida de Entropía Cruzada, Pérdida Logística, Pérdida Cuadrada, etc.
• Algoritmo de optimización: Adam, SGD, BFGS, etc.
• Métrica de evaluación: Recall, Precisión, Mínimos Cuadrados, etc.

Funcion de costo

Para cuantificar las errores del modelo en la optimizacion, se necesita una funcion de costo que llamamos $\ell$ . Ella representa si el modelo esta dando las buenas respuestas $y$ segundo una entrada $X$ . Este funcion penaliza el modelo cuando comete errores, y lo que queremos hacer es optimizar los pesos del modelo, para obtener una valor minimum de este costo, lo que significaria menos errores, entonces mejor modelo.

Hay que minimizar esta función sobre el conjunto de entrenamiento (riesgo empírico) para encontrar parámetros del modelo satisfactorios:

Los parametros van a cambiar para tener un valor minimum de costo: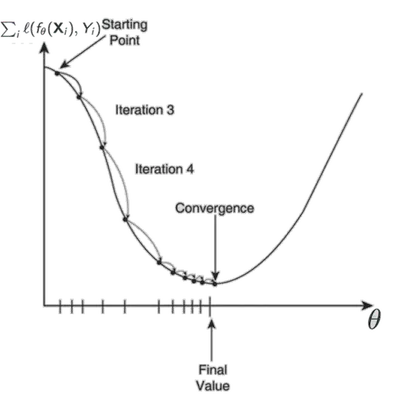

• La funcion de costo expresa el error desde una perspectiva numérica
• Transmite al algoritmo de aprendizaje lo que es importante y tiene sentido para la tarea
• Debe ser una función que se pueda optimizar eficientemente (convexa). La función $\ell^{0/1} = \mathbf{1}_{f(\mathbf{X}) = Y}$ no es utilizable (ni siquiera continua).

Complejidad de los modelos y sobre/soto-aprendizaje

• $\mathcal{F} = \{ f: \text{ funciones medibles } \mathcal{X} \text{→} \mathcal{Y}\}$
• Mejor solución $f^* = \arg\min_{f \in \mathcal{F}}\mathcal{R}(f)$
• Clase de funciones $\mathcal{S} \subset \mathcal{F}$ utilizadas como modelos
• Objetivo ideal en $\mathcal{S}$: $f^*_\mathcal{S} = \arg\min_{f \in \mathcal{S}}\mathcal{R}(f)$
• Estimación obtenida en $\mathcal{S}$ : se obtiene $f_\mathcal{S}$ tras un entrenamiento

Se pueden encontrar dos maneras de no tener el riesgo minimum optimum:

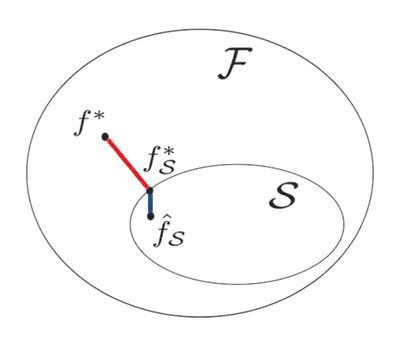
El error de aproximación puede ser grande si el modelo $\mathcal{S}$ no es adaptado, y el error de estimación puede ser grande si el modelo es complejo.

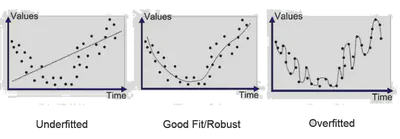
• Soto-aprentizaje: Si no hay demasiado parametros, es imposible de estimar bien la curva,
• Sobre-aprentizaje: Si hay demasiado parametros va a enfocar en memorizar el ruido del ensemble de entrenamiento

Regularizacion y parsimonia

Una solucion para combatir el problema de no generalizacion es la regularizacion, que permite de agregar una penalización en relación con la complejidad del modelo:

Hay varias posibilidades de penalizacion, generalmente se usa la norma de los pesos del modelo. La intuicion detras de eso es que disminuir la norma del modelo o su número de coeficientes, número de ramas del grafo (poda).

• AIC: $pen(\theta) = \lambda ||\theta||_0$ (no convexa, parsimoniosa, poco utilizada)
• Ridge: $pen(\theta) = \lambda ||\theta||_2$ (convexa, no parsimoniosa)
• Lasso: $pen(\theta) = \lambda ||\theta||_1$ (convexa, parsimoniosa)
• Elastic Net: $pen(\theta) = \lambda_1 ||\theta||_1 + \lambda_2 ||\theta||_2$ (convexa, parsimoniosa)

El $\lambda$ es un nuevo hiperparametro del modelo.

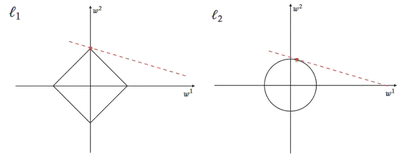
El lasso induce la parcimonia. Aca se pueden ver para $n=\{0,1,2\}$ , las bolas $$\mathcal{B}^n = \{x / x \in \mathbb{R}^d \text{ and } ||x||_n < 1\}$$ :

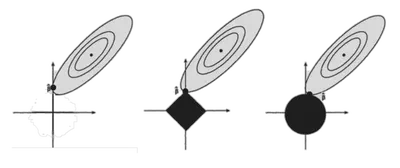
En dimensiones grandes, la mayoría de $\mathcal{B}^1$ se concentra en los ejes: esto equivale a tener valores nulos para otros ejes.

Optimizacion, loss landscape

La optimizacion de la funcion de costo sobre el ensemble de entrenamiento ( $ \frac{1}{n}\sum_{i=1}^n \ell(Y_i, f_\theta(\mathbf{X}_i) )$ ) se puede hacer de manera analitica en casos simples, o de manera iterativa. La fase de optimizacion va a hacer converger los parametros para encontrar los que van a dar un costo minimum en el conjunto de datos de entrenamiento.

En este ejemplo se puede ver los parametros $a,b$ del modelo $y = a\mathbf{X}+b$ cambiar por cada iteracion, para tener un valor del error (sse; suma residual de cuadrados) que esta diminuando: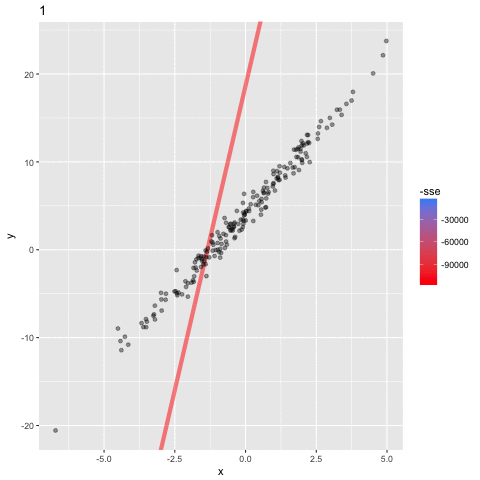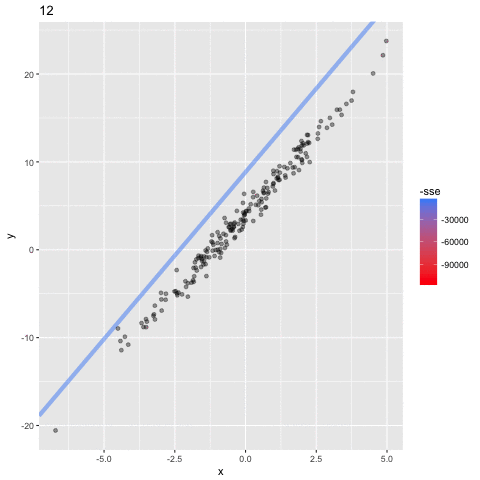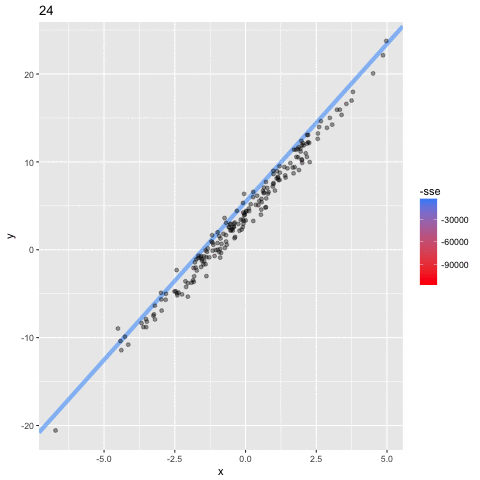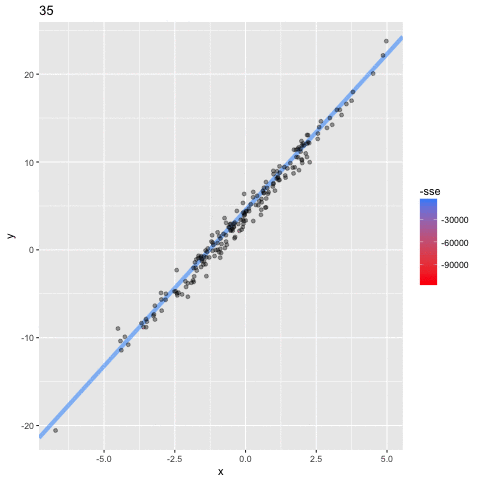

Porque la valor del costo empirico $ \frac{1}{n}\sum_{i=1}^n \ell(Y_i, f_\theta(\mathbf{X}_i) )$ es un nombre real positivo, podemos representarlo en un eje, y los parametros con unos otros ejes. Eso se llama el loss landscape:

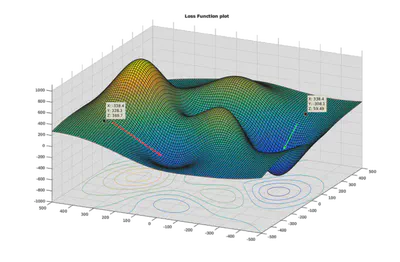
El objetivo del algoritmo de optimizacion es de encontrar la “ruta” para conducir en una “valle”, que representa un minimum local o global. Este ollo significa que los parametros sean los que dan un error pequeña.

Gradiente descendiente

El gradiente de una función $\nabla_xf(x)=(\frac{\partial f}{\partial x_i})_{i=1..n}$ es su derivativa según cada dimensión. Es una aproximación lineal de la función al nivel local. Este indica la direccion donde aumenta una funcion:

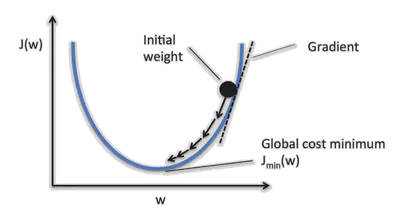
Por eso, se puede utilizar el gradiente de la funccion de costo para minimizar el costo. Después de cada cálculo de la función de costo $\ell(Y_i, f_\theta(\mathbf{X}_i) ; \theta)$ , se calcula el gradiente de esta función para actualizar los parámetros $\theta$ :

La tasa de aprendizaje $\alpha$ en la ecuacion precedente representa la cantidad de acutalizacion de los parametros. Es importante porque va a influir sobre la convergencia.

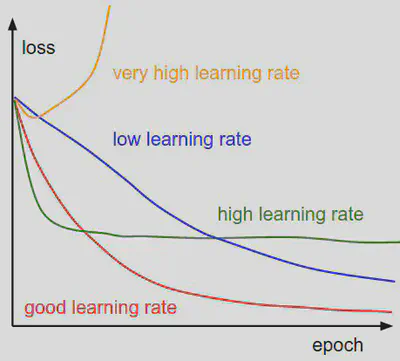
En en loss landscape, se puede representar el modelo durante la optimizacion como un vector moviendo en cada iteracion. Con este vision, la tasa de aprendizaje define mas o menos la “velocidad” de como se mueve este punto. Por eso, es simple de entender que a veces tiene que ser mas grande y otra veces mas pequeño, por ejemplo para pasar topografias particular del landscape.

Hay varios algoritmos de tipo gradiente descendiente para converger, con una mejora aproximacion de la tasa de aprendizaje, o la utilizacion de un momentum para ayudar el modelo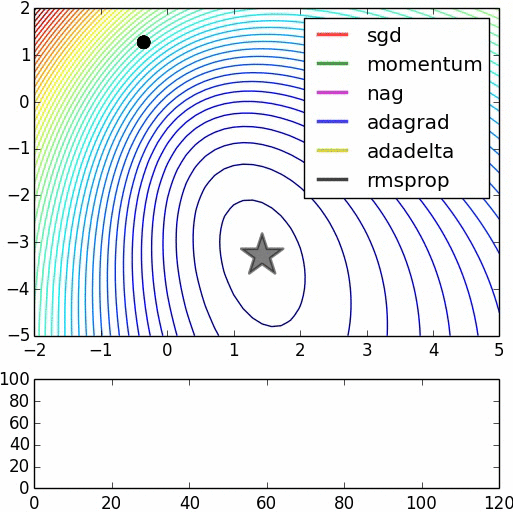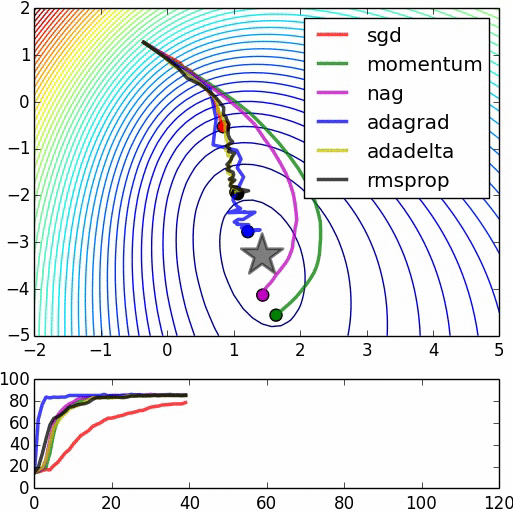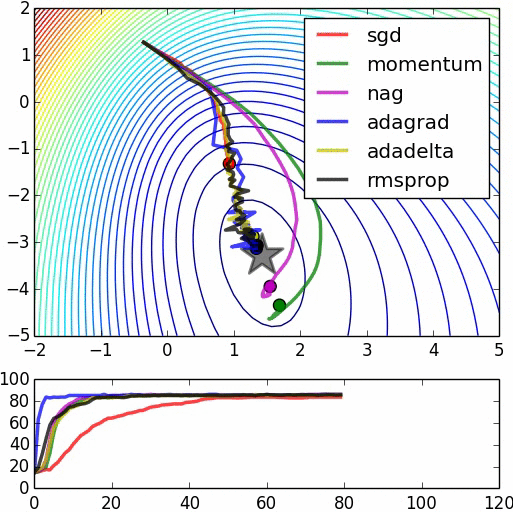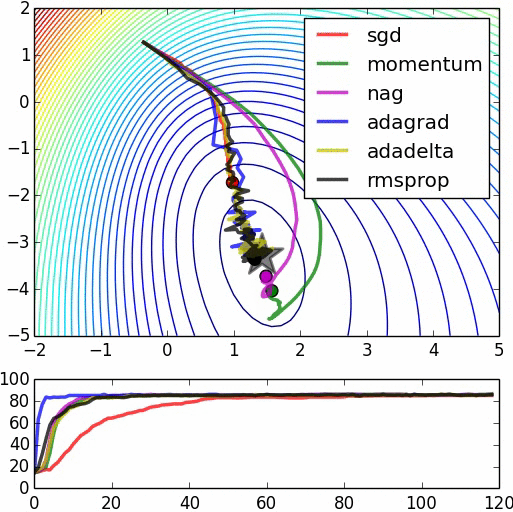

Metricas

Tipos de errores

Un clasificador binario debe detectar un evento. A cada prediccion puede tener una prediciccion verdadera o falsa: eso son los True/False Positives/Negatives: True Positive (TP), False Postiive (FP), False Negative (FN), True Negative (TN). Se pueden encontrar dos tipos de errores:

Con eso se puede crear una matriz de confusion.

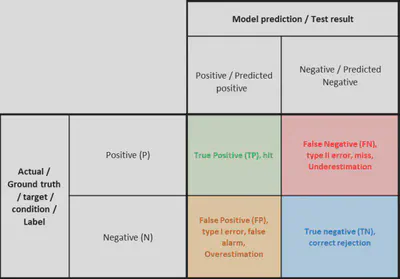
Las matrices de confusion pueden abarcar mas de 2 clases:

>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred) 
array([[2, 0, 0],
       [0, 0, 1],
       [1, 0, 2]])

Se puede cada vez volver a una binaria: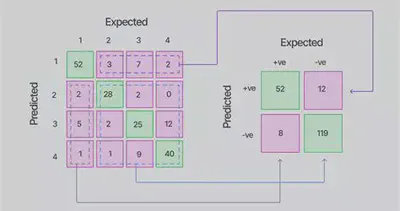

Tipos de metricas y costo

Usando los True/False Positives/Negatives, se puede calcular varias metricas segundo el tipo de applicacion. Tenemos: el accuracy al nivel general, y el recall, la precision y el F-score al nivel de las clases. Mas informacion por alla.

Cada tipo de error puede tener un costo differente segundo si es importante o no en la applicacion del sistema. Por eso se puede utilizar un matriz de costo, y calcular un costo global del sistema.

Aggregacion

Se puede agregar las metricas que son al nivel de clase para obtener un valor general:

• Macro-averaging: computar métrica para cada clase y luego promediar
• Micro-averaging: crear matriz de confusion binaria para cada clase, combinar las matrices y luego evaluar
• Weighted-averaging: computar métrica para cada clase y luego promediar usando pesos segun el importancia de la clase (nombre de ejemplos)

Here is a simple example in python obtained by the sklearn.metrics.classification_report function:

>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 2]
>>> y_pred = [0, 0, 2, 2, 1]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))

              precision    recall  f1-score   support

     class 0       0.50      1.00      0.67         1
     class 1       0.00      0.00      0.00         1
     class 2       1.00      0.67      0.80         3

    accuracy                           0.60         5
   macro avg       0.50      0.56      0.49         5
weighted avg       0.70      0.60      0.61         5

ROC & AUC

Al momento de la inferencia, nuestro clasificador binario va a dar una probabilidad que un ejemplo sea de la clase positiva. Generalmente, si es superior a $\tau = 0.5$ , significa que el ejemplo es de la clase positiva. Sin embargo, se puede jugar con este umbral $\tau$ .

El ROC (Receiver Operating Characteristic) es une curva representando la performancia de un clasificador en varias situaciones y que se crea variando el umbral. Para varios valores de el umbra, se calcula la fraccion de verdaderos positivos de los positivos frente a la fraccion de falsos positivos de los negativos.

El Area Under Curve (AUC) permite de obtener una unica valor representando la calidad de la curve. Mas grande significa mejor.

Regresion

Para una regresion, se utilizan metricas que que evaluan las distancias, y si el modelo representa bien la varianza de los datos:

• Varios calculos de errores
• Coeficiente de determinacion $R^2$ representa la proporcion de la varianza explicada

Tecnicas de evaluacion

Validacion Cruzada (Cross-Validation)

Para obtener una mejora estimacion de las performancias del modelo. Para estar seguro de testear sobre cada datos, se puede hacer $V$ experiencias, cortando el dataset en $V$ partes, entrenar sobre $V-1$ y testear sobre $1$ . Es un tipo de bootstrapping con los datos.

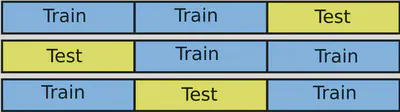
Eso sirve para obtener los hiperparametros optimum, antes de entrenar el model final sobre todos los datos, y estimar las performancias sobre el ensemble de test.

Conjuntos de validacion y prueba (Holdout)

Si es imposible de hacer una validacion cruzada (porque el entrenaimento es largo), se puede crear un set de entrenamiento, de validacion, y de test.

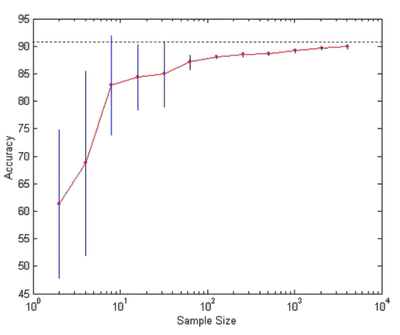
Tamaño de la particion

Un modelo que es buena usando pocos datos es interesante porque a veces obtener etiquetas puede ser costozo. Generalmente las perfomancias son mas variables y mas bajas con pocos datos de entrenamiento, pero la evaluacion es mas confiable con mas datos de test.

See you in the classroom!