Redes Neuronales

The slides are available here!

Perceptrón

Las Redes Neuronales se inspiran ligeramente en la biología de las neuronas, tratando de simular cómo la señal fluye entre capas de neuronas. El Perceptrón es la unidad básica que originó muchos avances en este campo.

¿Por qué este nombre?

En biología, una neurona:

Recibe neurotransmisores por las dendritas, provenientes de sinapsis de otras neuronas.
Se activa al superar un cierto umbral de estimulación.
Emite a su vez señal eléctrica por el axón, y libera neurotransmisores en sus sinapsis.

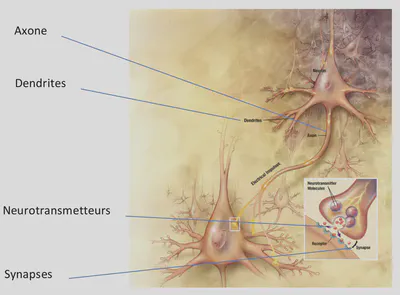
Esquema de neurona biológica — Las dendritas reciben información; si supera un umbral, la neurona dispara por el axón.

En un perceptrón:

Las entradas (análogo de dendritas) se combinan con ciertos pesos (\(w_i\)) y pasan por una función de activación que decide si hay salida (dispara) o no.
Si supera un umbral, la “neurona” artificial se activa.

Perceptrón: Presentación

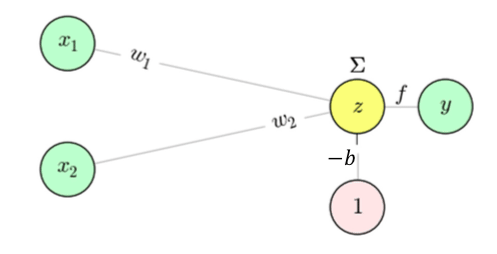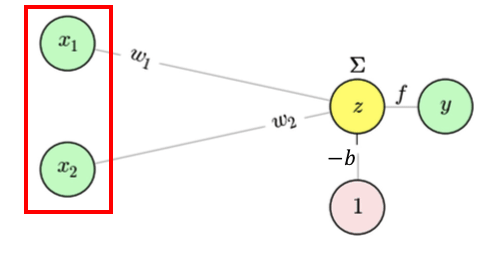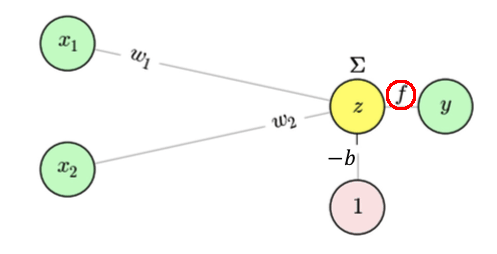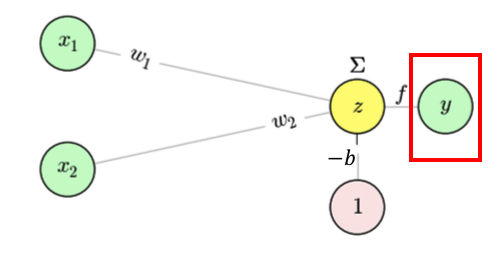
El perceptrón más simple (con dos entradas \(x_1\) y \(x_2\)) se representa como:

Un suma ponderada \(\sum_j x_j w_j - b\)
Una función de activación f que decide la salida \(y\).

En la versión binaria más elemental:

\[ y = f\bigl(x_1 w_1 + x_2 w_2 - b\bigr) = f\bigl(W^TX- b\bigr) \]

Donde \(f\) es (en teoría) la función Heaviside:

\[ f(z) = \begin{cases} 1, & z \ge 0\\ 0, & z < 0 \end{cases} \]

Si \(x_1 w_1 + x_2 w_2 \) supera el umbral \(b\), la salida es \(1\).

Algunas representaciones gráficas:

Perceptrón con umbral binario — El perceptron, con la capa de entrada \(X\), la funcion de activacion \(f\), la salida \(y\)

Perceptrón Multicapa (MLP)

Para resolver tareas más complejas, se agregan capas de neuronas:

Capa de entrada: Recibe las características (\(x\) o \(\mathbf{a}^{(1)}\)).
Capas ocultas: Transforman la información de forma intermedia.
Capa de salida: Emite la predicción final (clase, valor, etc.).

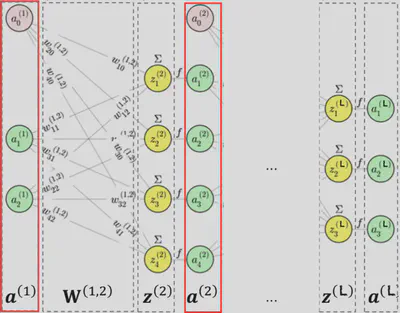
Ejemplo de un MLP

La señal va propagándose hacia adelante, capa por capa (“feed-forward”):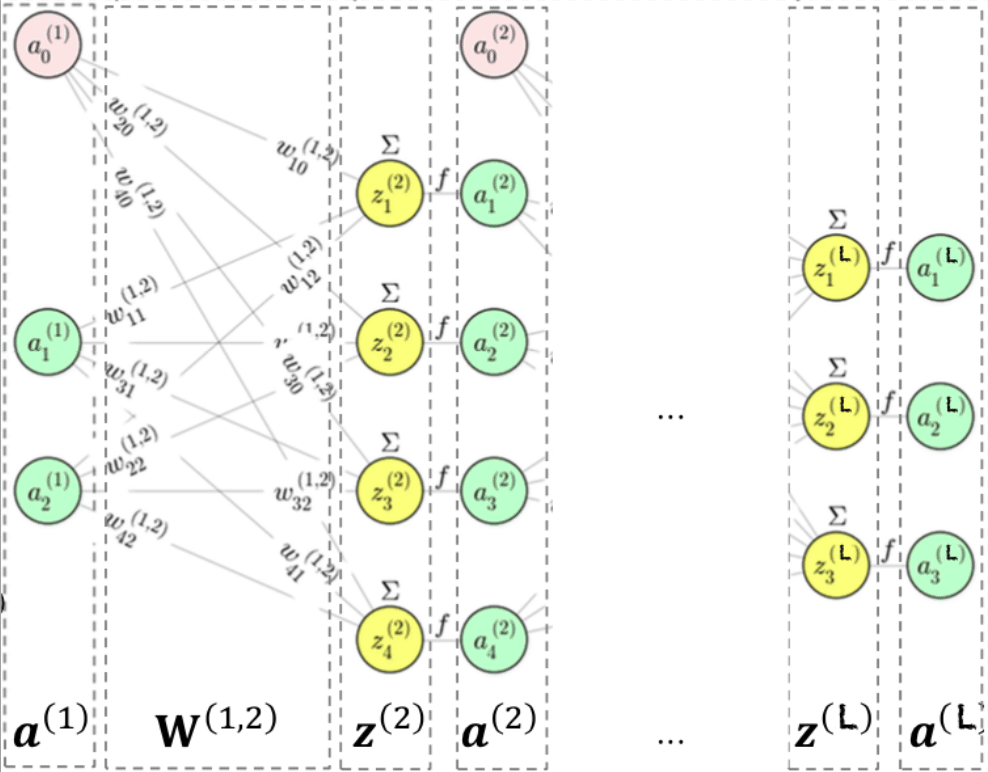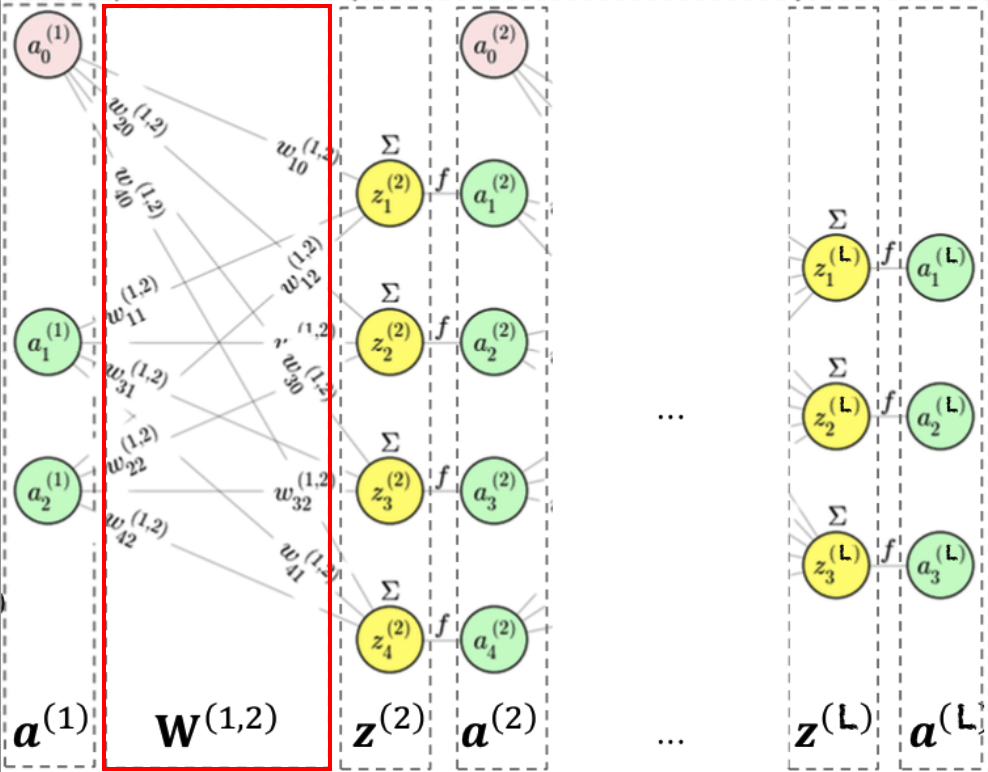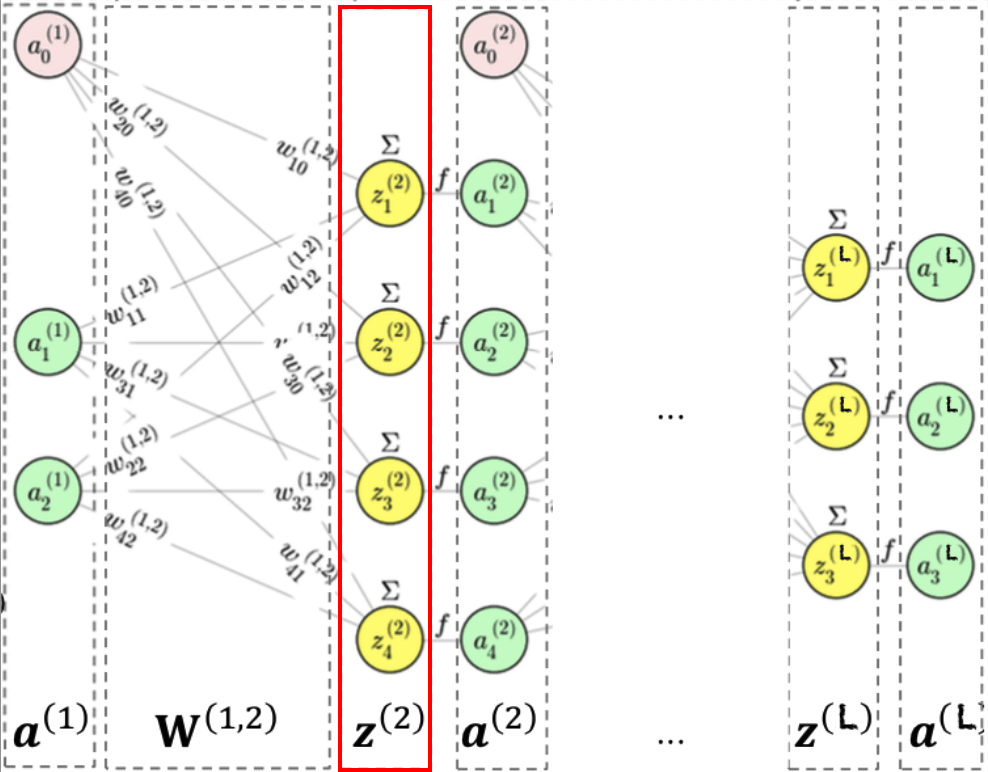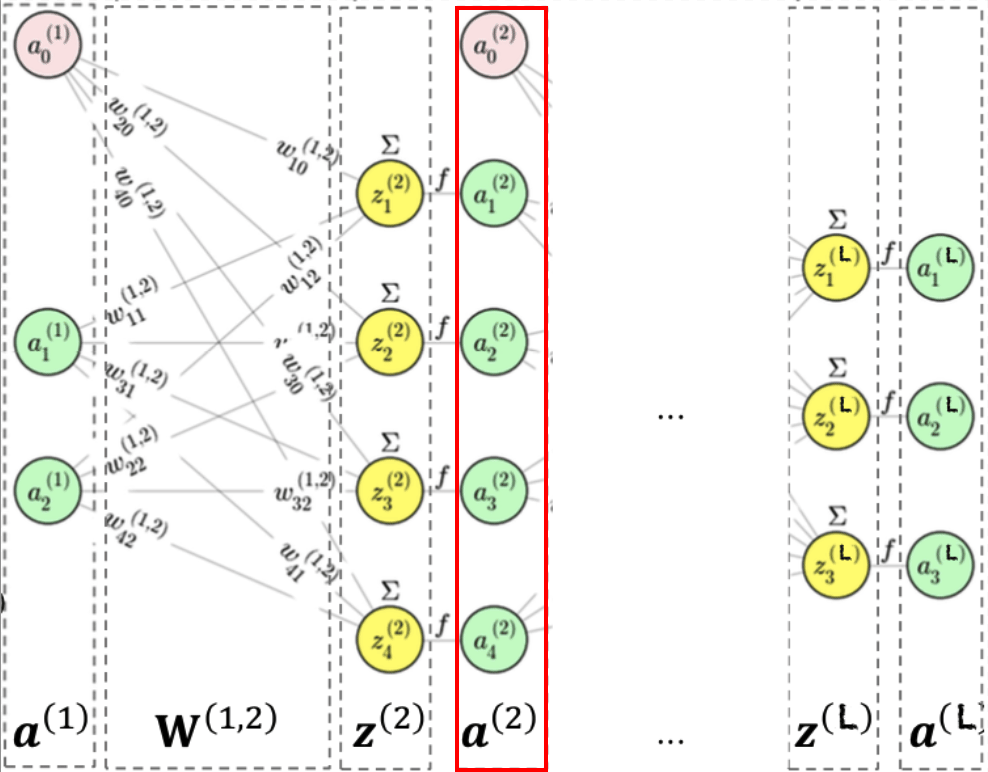

MLP de 2 capas ocultas — Propagación en un MLP, con 2 capas de neuronas intermedias

Ecuaciones y Composición

Principio de una capa

Si la capa \(\ell\) tiene \(n_\ell\) neuronas, y recibimos como entrada \(\mathbf{a}^{(\ell)}\), la salida \(\mathbf{a}^{(\ell+1)}\) se obtiene aplicando:

\[ \mathbf{a}^{(\ell+1)} = f\bigl( \mathbf{W}^{(\ell,\ell+1)} \; \mathbf{a}^{(\ell)} \bigr) \]

donde \(f\) es la función de activación elemento a elemento, y \(\mathbf{W}^{(\ell,\ell+1)}\) es la matriz de pesos entre la capa \(\ell\) y la capa \(\ell+1\).

Por ejemplo, para una sola neurona \(j\) en la capa \(\ell+1\):

\[ a_j^{(\ell+1)} = f\Bigl(\sum_i w_{ji}^{(\ell,\ell+1)} \; a_i^{(\ell)}\Bigr) \]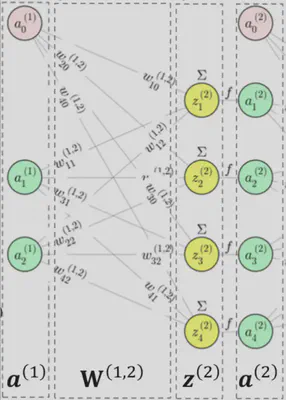

Ejemplo de una capa con 4 neuronas de salida

MLP: composición de capas

Un MLP con \(L\) capas puede verse como una composición de funciones:

\[ \mathbf{a}^{(2)} = h^{(1,2)}(\mathbf{a}^{(1)}), \quad \mathbf{a}^{(3)} = h^{(2,3)}(\mathbf{a}^{(2)}) \quad \ldots \quad \mathbf{a}^{(L)} = h^{(L-1,L)}(\mathbf{a}^{(L-1)}). \]

Por tanto:

\[ \mathbf{a}^{(L)} = h^{(L-1,L)} \circ \cdots \circ h^{(1,2)}\;(\mathbf{a}^{(1)}). \]

Esta \(\mathbf{a}^{(L)}\) es la salida final del MLP.

Se puede escribir una funcion del MLP:

\[ MLP = h^{(L-1, L)} \circ h^{(L-2, L-1)} \circ ... \circ h^{(1,2)} \text{ \textbf{tal que} } MLP(\mathbf{a}^{(1)}) = \mathbf{a}^{(L)} \]

Conclusión: un MLP es una función no lineal compuesta. A mayor número de capas (profundidad), mayor capacidad de representar funciones complejas.

Funciones de Activación

La función de activación en cada neurona rompe la linealidad. Sin ella, el modelo sería solo una combinación lineal de los datos. Algunas funciones típicas:

Nombre	Gráfico	Ecuación	Valores en \(\pm\infty\)	Valores derivada en \(\pm\infty\)
Heaviside (teórica)	[No derivable]	\(f(z)=\mathbf{1}_{z\ge0}\)	0,1	-
Sigmoide		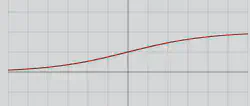\(f(z)=\frac{1}{1+e^{-z}}\)	0; 1	0; 0
Tanh		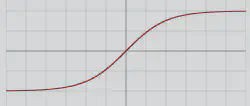\(f(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}\)	-1; 1	0; 0
ReLU		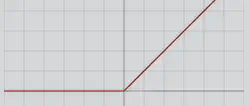\(f(z)=\max(0,z)\)	0; \(z\)	0; 1
ELU		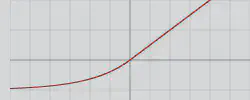\(f(z)=\begin{cases}\alpha(e^z-1)&z<0\\ z&z\ge0\end{cases}\)	\(-\alpha\); \(z\)	0; 1

Heaviside (original) no es derivable.
Sigmoide / Tanh: buenas para salidas en [0,1] o [-1,1], pero pueden saturarse.
ReLU: muy popular en redes profundas.
ELU: variante suavizada por debajo de 0.

Recuerdos de Optimización y Entrenamiento

Para entrenar la red, definimos una función de costo (\(\ell\)), por ejemplo el error entre salidas reales y predichas. Queremos minimizar esa función respecto de los pesos de la red.

Descenso del Gradiente

Si \(\theta\) representa todos los pesos:

\[ \theta \leftarrow \theta - \alpha \; \nabla_\theta \ell(\theta) \]

donde \(\alpha\) es la tasa de aprendizaje.

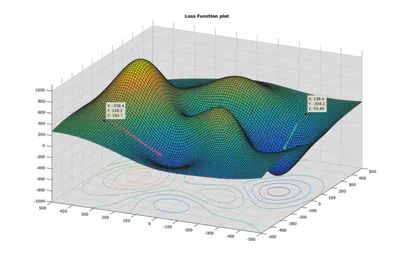
Convergencia en un valle del “paisaje de costos” — Visualización conceptual

Se pueden usar mini-batches (stochastic gradient descent - SGD) para computar gradientes parciales y hacer actualizaciones más frecuentes.

Backpropagation: el núcleo del entrenamiento

Backpropagation (o retropropagación del error) es el algoritmo que:

Calcula la salida de la red (forward pass).
Evalúa el error (función de costo).
Propaga gradientes hacia atrás (desde la salida a cada capa) usando la regla de la cadena.
Actualiza cada peso según su gradiente parcial.

Explicación más detallada:

Tras un forward pass, conocemos la salida \(\mathbf{a}^{(L)}\).
Comparamos con la etiqueta real y obtenemos el error \(\ell\).
Para cada capa \(\ell\), la derivada de \(\ell\) respecto a \(\mathbf{W}^{(\ell,\ell+1)}\) se computa recursivamente, empezando por la capa de salida y yendo hacia la capa de entrada.
Esto es posible gracias a que \[ \frac{\partial \ell}{\partial \mathbf{W}^{(\ell,\ell+1)}} = \frac{\partial \ell}{\partial \mathbf{a}^{(\ell+1)}} \cdot \frac{\partial \mathbf{a}^{(\ell+1)}}{\partial \mathbf{z}^{(\ell+1)}} \cdot \frac{\partial \mathbf{z}^{(\ell+1)}}{\partial \mathbf{W}^{(\ell,\ell+1)}}. \]
Se multiplican derivadas (regla de la cadena) y se obtiene la dirección de ajuste de cada peso.

Representación esquemática de backpropagation (imagen ilustrativa) — El error fluye hacia atrás para ajustar cada capa

En la práctica, librerías como PyTorch o TensorFlow hacen esto automáticamente mediante autograd.

Representaciones

En un MLP, cada capa oculta \(\mathbf{a}^{(\ell)}\) forma una representación distinta de los datos. Al componer varias capas, se construyen representaciones de nivel creciente de abstracción.

MLP con 2 capas ocultas y salidas intermedias (activaciones) — Cada capa genera un nuevo vector de características (activaciones)

En imágenes: capas iniciales detectan contornos, capas intermedias detectan partes (nariz, ojo…), capas finales reconocen objetos concretos.
En texto: capas iniciales identifican gramática, capas intermedias reconocen entidades, capas profundas comprenden significados complejos (sentimientos, intenciones…).

Composicionalidad de las representaciones

En CNN u otras redes, se pueden visualizar “filtros” que activan sobre patrones (bordes, texturas, etc.).

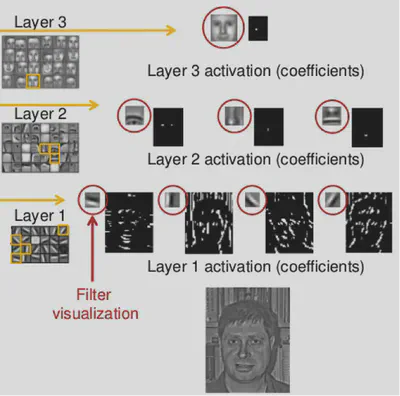
Visualización de filtros (composición de características) — Se compone con los filtros mas basicos los filtros mas complejos: una cara se compone de 2 ojos una nariz y una boca.

Visibilidad de filtros

Una video muy interesante de la Deep Visualization Toolbox para ver en tiempo real lo que activa los diferentes neuronas, las imagenes del dataset que les activan lo mas, y imagenes artificiales optimizada para activar los filtros.

La visualizacion de las imagenes que activan el mas los filtros de un AlexNet en Distill.pub: Feature Visualization:

Representation Learning for Transfer

Aprendizaje de Representaciones

El aprendizaje de representaciones (Representation Learning) se basa en que la red neuronal aprende, de forma automática, características o features útiles directamente desde los datos brutos (imágenes, texto, etc.). Estas capas ocultas (o embeddings) pueden:

Generalizar mejor que las características diseñadas a mano (hand-crafted features).
Adaptarse a distintas tareas si se transfieren.

Los intereses son varios, por ejemplo:

Cada capa proporciona una representación de los datos de entrada con dimensiones más bajas.
Esas representaciones provenientes únicamente de los datos brutos a veces superan conjuntos de descriptores clásicos \(\rightarrow\) Youtube-8M: Representaciones con LogReg superaban a todos los clasificadores de vanguardia en muchas tareas.

t-SNE de representaciones de AlexNet — Las representaciones en altas dimensiones se proyectan a 2D y muestran agrupaciones naturales.

(Ejemplo: después de entrenar en ImageNet, las capas profundas “entienden” rasgos básicos de las imágenes. Si queremos clasificar perros vs. gatos, basta con re-entrenar poco.)

Transferencia

Una red entrenada en una tarea (p. ej. reconocimiento de objetos en imágenes) puede servir como base para otras tareas (p. ej. detectar nuevos tipos de objetos). Se aprovecha el transfer learning:

Entrenamos una red (p. ej. CNN) en una gran base (ImageNet).
Se “toman” sus capas iniciales como extractor de características (al estar entrenadas en millones de imágenes, captan contornos y patrones generales).
Para una nueva tarea con pocos datos, se conectan la capa final (llamado head) nueva o se re-entrena ligeramente (fine-tuning).

De este modo, la representación (las activaciones intermedias) es reutilizada. Esto ahorra tiempo y datos: